牛顿法（Newton's method）学习

牛顿法是一种在实数域和复数域上迭代近似求解方程的方法。 此处做一个简单的学习。

牛顿法能做什么？直观上怎么做的？

一般来说，牛顿法主要用在两个方面:

1. 求方程的根：通过当前解与函数的切线在 x 轴的交点迭代更新解值，以求得方程的解。
2. 最优化：最优化问题通常可以理解为求函数导数的解（导数值为0），则可以使用 1 中求方程的根的方法。

一个简单的过程示意图如下所示：

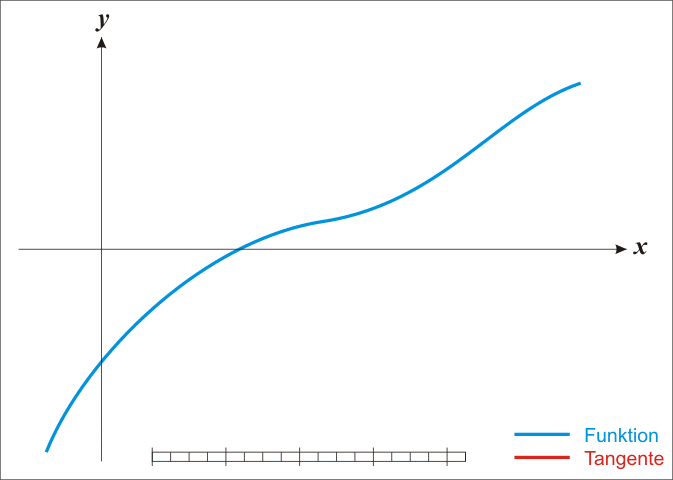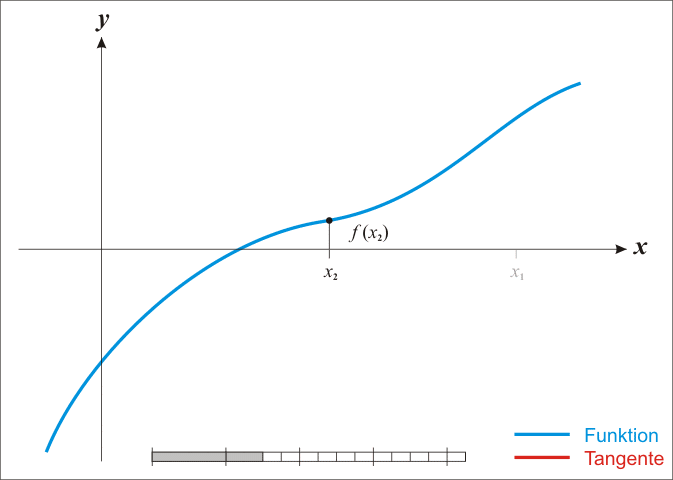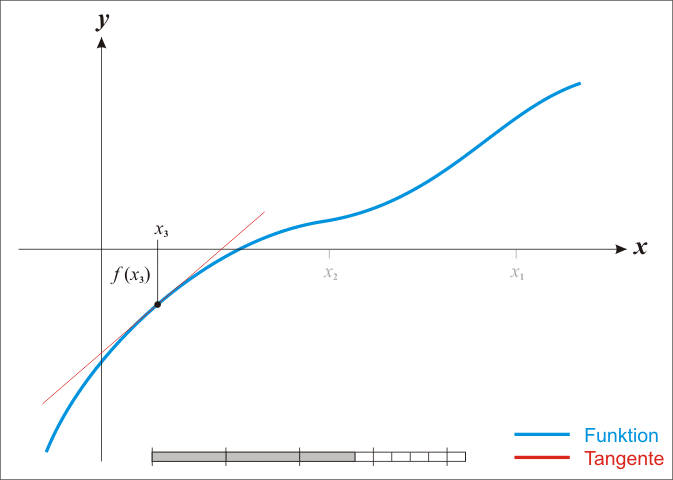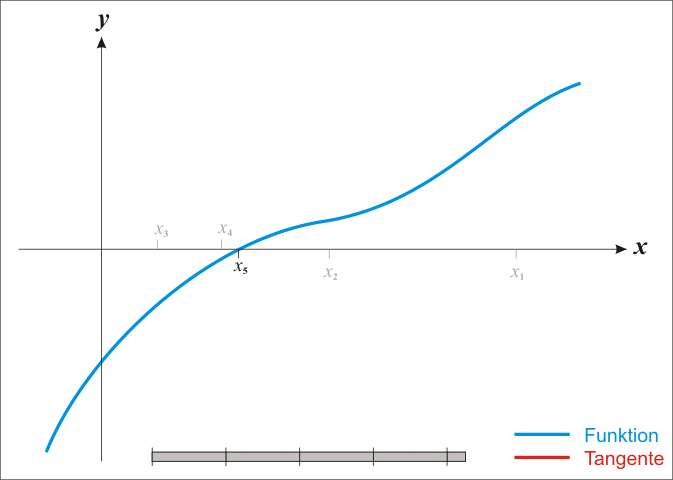
具体来说怎么做？

求解方程时，迭代更新 $x$。

$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime}\left(x_n\right)}$$

最优化时，迭代更新 $x$。

$$x_{n+1}=x_n-\frac{f^{\prime}\left(x_n\right)}{f^{\prime \prime}\left(x_n\right)}$$

有什么特点？

牛顿法最突出的优点是收敛速度快，具有局部二阶收敛性。 通俗来说梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，而牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。 所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。

有什么局限性？

1. 基本牛顿法初始点需要足够“靠近”极小点，否则有可能导致算法不收敛。这样就引入了全局牛顿法。
2. 在牛顿法的迭代中，需要计算海森矩阵（函数的二阶导数）的逆矩阵，这一计算比较复杂，这样就引入了拟牛顿法，用一个矩阵来替代。
   • DFP(Davidon-Fletcher-Powell)算法(DFP algorithm)
   • BFGS(Broyden-Fletcher-Goldfard-Shano)算法(BFGS algorithm)
   • Broyden类算法(Broyden’s algorithm)

Reference

1. 梯度下降法、牛顿法和拟牛顿法 - Eureka的文章 - 知乎
2. 牛顿法