再次学习强化学习的笔记

距离上一次学习强化学习已经很久了。 最近由于 learning to optimize 用到了很多强化学习的知识，猛的一看发现又不太懂，于是这里进行对于强化学习的再学习。 上一次对强化学习的学习见这一篇帖子。

总的来说，上次对于强化学习的理解过于浅薄，而且并没有从一个系统性和直观的角度进行理解，导致抄了一堆公式也是白抄。 本文主要以一个直观的角度来对一个重要算法在整个体系中存在的位置做一个定位，不会过多陷入数学计算。

什么是强化学习？（一些基础知识）

强化学习目标是学到一个对于目标任务的策略 policy ($\pi$)，给定一个当前的状态 state ($s$)，策略可以给出当前应该执行的策略 action ($a$) 以获得最大收益。

此外还有以下一些概念：

• Value 价值：一般单独提到时指的是当前状态的价值。
• Q-value 动作价值：指在某一个状态 $s$ 下实施动作 $a$ 所能收获的收益。
• Model 模型：指状态转移的模式，即环境对于特定的动作如何反应。
• Return 回报：指在整个交互结束之后能收到的总奖励。

最初的方法： Q-Leaning & Policy Gradient

我们这里还是更多的介绍一下 model-free 的场景。 具体来说，我们对环境提供的状态转移无知，并且我们不对其进行建模。 在这种情况下，我们想要学习一个策略，$\pi(s)\rightarrow a$，可以有两种方式：

1. 学习不同状态下的 Q-value，并对其进行建模。建模成功之后即可选取在当前 state 下 Q-value 最大的 action 实施。
2. 直接学习策略 $\pi$，则可直接输入 state，得到 action。

那么两者各有什么特点呢？

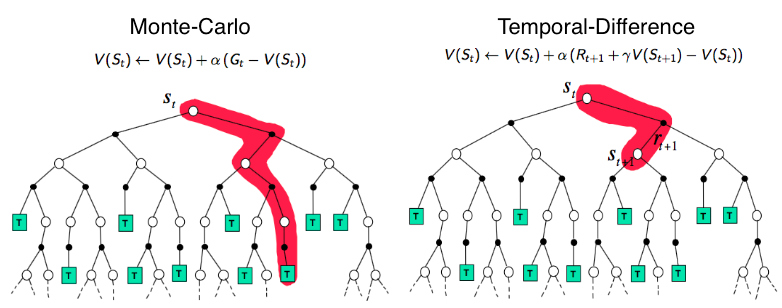
1. Q-learning 以值为基础，可以使用时序差分（temporal-difference）的思路，使效用估计朝着理想均衡方向调整，可以进行单步更新。但是由于其离散化的特点，如果在连续空间中进行选择，则会瘫痪。
2. Policy gradient 可以在毫不费力地在连续空间中进行选择，但是因为其是基于 Monte-Carlo 采样得到的评估，必须等一个回合结束后才可以更新，学习效率低。

结合两者的优点 Actor-Critic

Policy gradient 使用现实中的奖惩来更新 actor。 此时的梯度可以写作：

$$\nabla \bar{R}_\theta=E_{\tau \sim p_\theta(\tau)}\left[R(\tau) \nabla \log p_\theta(\tau)\right]$$

这个 reward 奖惩信息 $R$ 可以被学出来，作为一个 critic 来来指导 actor 训练。 Critic 可以看到当前所处状态动作的潜在奖励，所以可以使得 actor 每一步都在更新，而不是到回合结束才能更新。 AC 中的梯度可以写作：

$$\nabla \bar{R}_\theta=\frac{1}{N} \sum_{n-1}^N \sum_{t=1}^{T_n} Q^{\pi_\theta}\left(s_t^n, a_t^n\right) \nabla \log p_\theta\left(a_t^n \mid s_t^n\right)$$

A2C 和 A3C

Advantage Actor-Critic (A2C)

AC 中使用 Q-value，方差大，梯度差异较大训练不稳定。 PG 中同样有这种问题，它的解决方式是引入一个 baseline，用累计奖励 Gain 减去 baseline，可以使梯度减小，训练平缓。

$$\nabla \bar{R}_\theta=\frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n}\left(Gain_t - baseline(s_t)\right) \nabla \log p_\theta\left(a_t^n \mid s_t^n\right)$$

A2C 中，认为对于 Q-value $Q^{\pi_\theta}\left(s_t^n, a_t^n\right) $ 一个自然的 baseline 选择是 $V^{\pi_\theta}\left(s_t^n\right)$。 于是可以构造优势函数 advantage function $A(s_t,a_t) = Q(s_t,a_t)-V(s_t)$。 其可以通过近似计算得到 $A(s_t,a_t) = r_t^n+V^\pi\left(s_{t+1}^n\right)-V^\pi\left(s_t^n\right)$。 所以可以仅用一个网络来估计 $V$ 值而不用评估 Q-value。 可以说 A2C 解决的是梯度方差大，训练不稳定的问题。

A2C 中的梯度可以写作：

$$\nabla \bar{R}_\theta=\frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} A^{\pi_\theta}\left(s_t^n, a_t^n\right) \nabla \log p_\theta\left(a_t^n \mid s_t^n\right)$$

除了方差大，AC 还存在的问题：两个网络交替训练，critic 和 action 强相关，有着很强的时序关联，只能探索到有限的状态和动作空间。 为了打破经验耦合，需要采用 experience replay，使得 agent 在后续训练可以访问到以前知识（例如 DQN 和 DDPG（DQN+AC）这类基于值的方法）。 但是策略类的方法，经验都是以 episode 形式获得，用完即弃。

在此情况下使用并行架构，不同的 worker 与环境进行交互，得到独立的采样经验。 即每轮训练中，Global network 都会等待每个 worker 各自完成当前的 episode，然后把这些 worker 上传的梯度进行汇总并求平均，得到一个统一的梯度并用其更新主网络的参数，最后用这个参数同时更新所有的 worker。 可以说 A2C 也解决了经验耦合的问题。

Asynchronous Advantage Actor-Critic (A3C)

A3C 相对于 A2C 使用了异步经验更新。 没有等待所有 worker 完成当前 episode 并汇总的过程。

各个 worker 都分别使用着一套不同的策略，独立的跟自己的环境交互。而主网络保持着最新的策略，各 worker 跟主网络同步的时间也是不一样的，只要有一个 worker 完成当前episode，主网络就会根据它的梯度进行更新，并不影响其它仍旧在使用旧策略的 worker。这就是异步并行的核心思想。

但是研究者们逐渐发现A3C主要优势在于采用了“并行训练”的思想，而不一定要“异步地并行训练”。 异步更新并没有使训练效率和性能取得显著提高【3】，A2C 表现更好（A2C 是在 A3C 后面出现的）。

结语

本文并没有深入技术细节，而是从强化学习（在这几个方法上）的演变角度，简单的记录了不同方法的 intuition。 比之前的学习笔记或许在问题定义上清晰了一些。

Reference

1. 什么是 Actor-Critic (强化学习) - 莫烦的文章
2. 深入理解强化学习（七）- Actor-Critic - 莫冉的文章
3. 深度强化学习 – 进击的 Actor-Critic（A2C 和A3C） - Quantum cheese的文章
4. 强化学习AC、A2C、A3C算法原理与实现！ - 梁勇的文章
5. Actor-Critic的变体 - heaven的文章