机器学习中的 Lipschitz Continuity

在 discriminator 的学习使用中，经常会见到这个 Lipschitz Condition，在此处做一个学习。

Lipschitz Continuity

Lipschitz Continuous 是比可微分更严格的条件，这个性质限制了函数的微分值必须有上下限。 换句话说，目标函数会被一个一次函数上下夹逼，如下图所示。

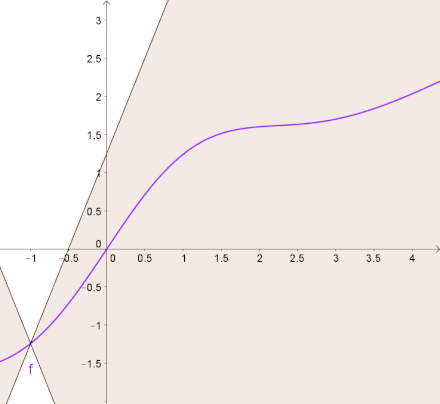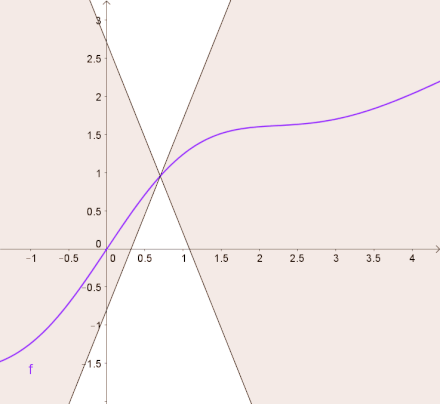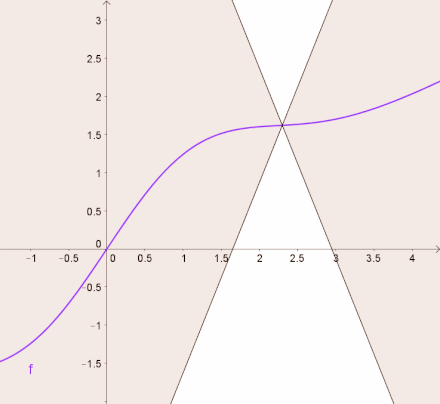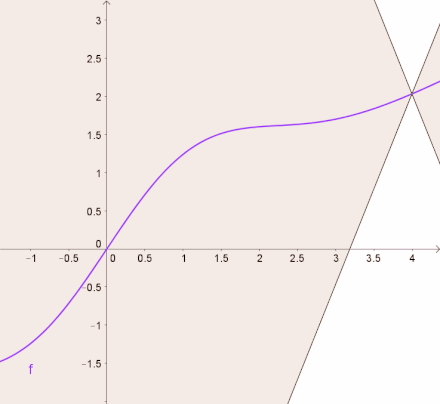
以公式的形式展开，函数需要满足以下条件：

$$\|f(x)-f(y)\| \leqslant L\|x-y\|$$

为什么会在机器学习中使用？

本人目前见到过的使用地点多在 discriminator 相关工作中。 Discriminator 在 GAN 相关模型中是一个必要的结构，在域迁移的模型中也多有使用。 其作用是将真实样本与虚假样本分开，之后在将其固定来训练生成器使得判别器无法将虚假样本分开。

当下 GAN 可以生成足以骗过人类的高质量图像，但是其训练过程的不稳定仍然是一个具有挑战性的问题。 因此，一系列的研究工作都着眼于解决不稳定训练的问题。 WGAN 中使用 wasserstein distance 来代替原始 GAN 中的分类损失，效果良好。

$$\left(P_r, P_g\right)=\inf _{\gamma \in \prod\left(P_r, P_g\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|]$$

但是由于这个形式十分难以求解，所以将该优化问题转换为以下形式。

$$W\left(P_r, P_\theta\right)=\sup _{\|f\|_L \leq K} \mathbb{E}_{x \sim P_r}[f(x)]-\mathbb{E}_{x \sim P_\theta}[f(x)]$$

这个转化通过对判别器应用正则化或归一化，将判别器形式化定义为一个利普希茨连续的函数（Lipschitz continuous function），其利普希茨常数为 K。 这样，在不大幅度牺牲判别器性能的条件下，判别器的梯度空间会变得更平滑，可以更加稳定的训练。 在此技术上，有谱归一化和梯度归一化等工作。

Reference

• 舍弃谱归一化，这篇ICCV’21论文用梯度归一化训练GAN，效果极好
• 深度学习中的Lipschitz约束：泛化与生成模型
• What is Lipschitz constraint and why it is enforced on discriminator?
• Spectral Normalization 谱归一化-原理及实现