高斯过程 Gaussian Process

一份理解高斯过程的笔记。

参考：

• A Visual Exploration of Gaussian Processes
• 看得见的高斯过程：这是一份直观的入门解读
• 如何通俗易懂地介绍 Gaussian Process？
• 高斯过程回归：推导，实现和理解
• 深度学习基础（高斯过程）

高斯过程的简要理解

高斯过程可以被用于分类和回归问题，是一种非参数贝叶斯方法。 在 $k$ 个测试样本上预测的情况，可以想象成在一个 $k$ 维的高斯分布下进行采样。 在每个维度上的采样结果或者该维度的均值，可以当作在这个样本上的预测值。 所以说问题转化为如何构建这个 $k$ 维的高斯分布，一旦构建完成则可以用来回归预测。

直接对预测数据 $X^\ast$ 构建这个先验分布 $P(f(X^\ast))$ 是困难的，所以在有训练数据 $Y$ 的情况下，我们期望找到的是一个后验概率分布 $P(f(X^\ast)|Y)$。

多变量高斯分布

我们先从多变量高斯分布说起，介绍其形式和性质。

1. 先验分布

对于一个先验分布是高斯分布的一组随机变量 $X \sim \mathcal{N}(\mu,\,\Sigma)$， $X$ 可以由两部分组成 $X_a$ 和 $X_b$，代表原始随机变量的子集，维度为 $|X_a|+|X_b| = p + q$。

具体来说，

$$X=\begin{bmatrix}X_a\\X_b\end{bmatrix}_{p+q}\quad\mu=\begin{bmatrix}\mu_a\\\mu_b\end{bmatrix}_{p+q}\quad \Sigma=\begin{bmatrix}\Sigma_{aa}&\Sigma_{ab}\\\Sigma_{ba}&\Sigma_{bb}\end{bmatrix}_{p + q, p + q}$$

其中 $\mu$ 和 $\Sigma$ 是对应的均值和方差。

2. 通过先验分布得到后验分布

此时我们可以通过条件作用 conditioning 从 $P(X_a,X_b)$ 得到 $P(X_b|X_a)$。 这样是从一个维度为$|X_a|+|X_b|$的高斯分布得到一个维度为维度为 $|X_b|$ 的高斯分布。 以下是一个二维高斯分布的示意图，其中包含边缘分布以及条件分布的示意。

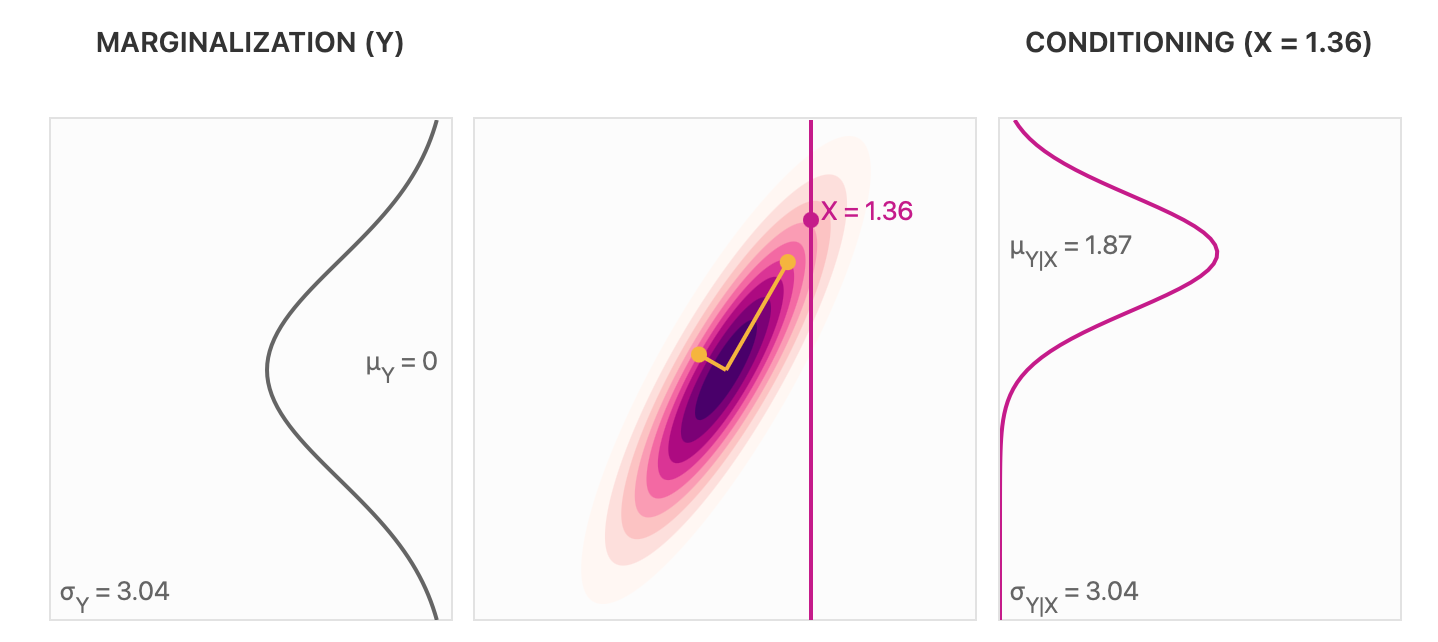
条件作用之后均值和标准差会发生变化，依据高斯分布的性质可以得到以下条件分布，

$$X_b|X_a \sim N(\mu_{b|a},\Sigma_{b|a})$$

其中， $\mu_{b|a}=\Sigma_{ba}\Sigma^{-1}_{aa}(X_a-\mu_a)+\mu_b$, $\Sigma_{b|a}=\Sigma_{bb}-\Sigma_{ba}\Sigma^{-1}_{aa}\Sigma_{ab}$。

总的来说，在由一系列随机变量组成的高斯分布中，可以得到其中一部分随机变量的条件分布（同为高斯分布的形式）。 这个分布的具体形式与条件作用中随机变量的取值、均值和协方差有关。

高斯过程

此时我们发现，在多维高斯分布中，我们已经可以通过条件概率得到特定随机变量的高斯分布了，这就是高斯过程用于预测的基础。 得到的高斯分布的均值可以用作预测值，方差可以用作预测的不确定性。 高斯过程就是一个定义在连续域上的无限多个高斯随机变量所组成的随机过程，我们想做的事是将这所有的无限多的随机变量表示出来。

那么类似的，我们首先需要建立起联合分布的高斯分布表达式，要定义均值和协方差矩阵 $\mu$ 和 $\Sigma$。

1. 均值 $\mu$，一般在数据归一化的情况下，先验均值可以设为 0 函数。
2. 对于协方差矩阵 $\Sigma$，则可以用核函数来生成。

核函数，一般用作一种距离的度量，可以理解为可以两个样本点的相互影响。 这里用现有样本的特征 $x$ 建立随机变量间的距离，再用其作为每个维度之间的协方差。 此处的核函数有多种选择方式，可以起到添加先验知识的作用。 此外，核函数还可以通过组合来使用，比如加法组合、乘法组合等，通常会获得一些合并的特性，比如既是周期又有线性。

在联合分布中，我们不仅要考虑待预测的测试样本点 $X^\ast$，还需要考虑观测的训练样本点 $X$（下图中黄色点）。 训练样本点限制了函数空间中的函数，使得我们可以得到一个更加合理的预测结果。

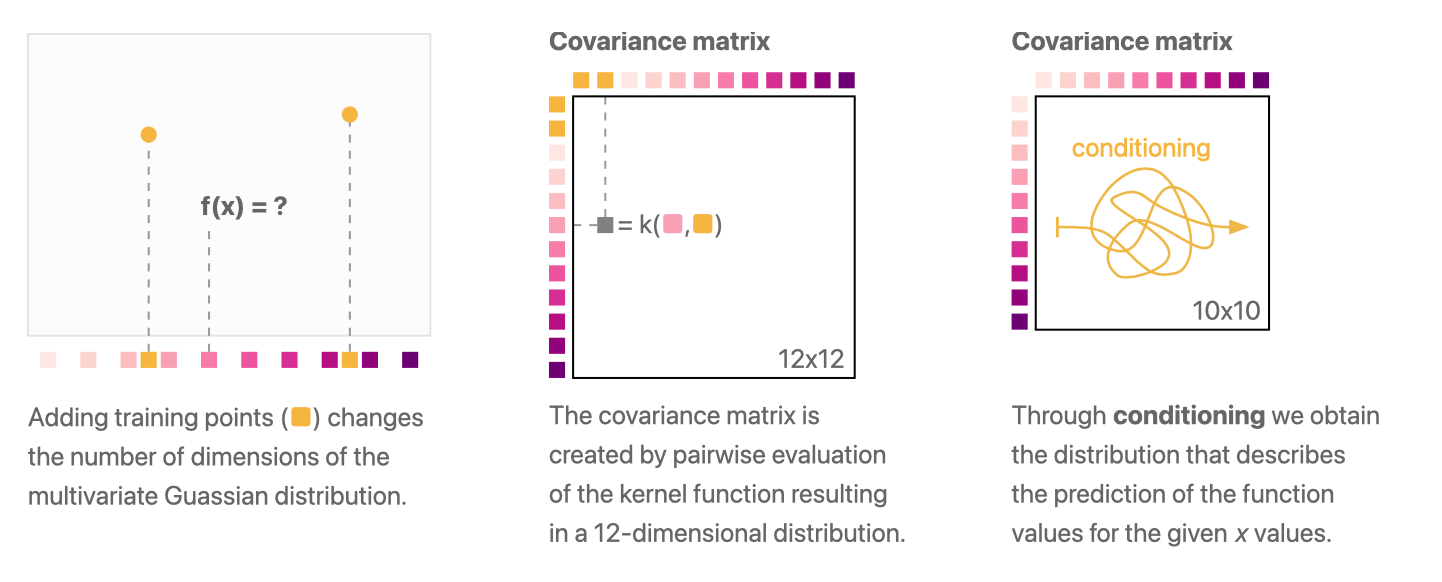
限制的效果如下图所示，可以看到在训练样本点附近的预测值更加准确。

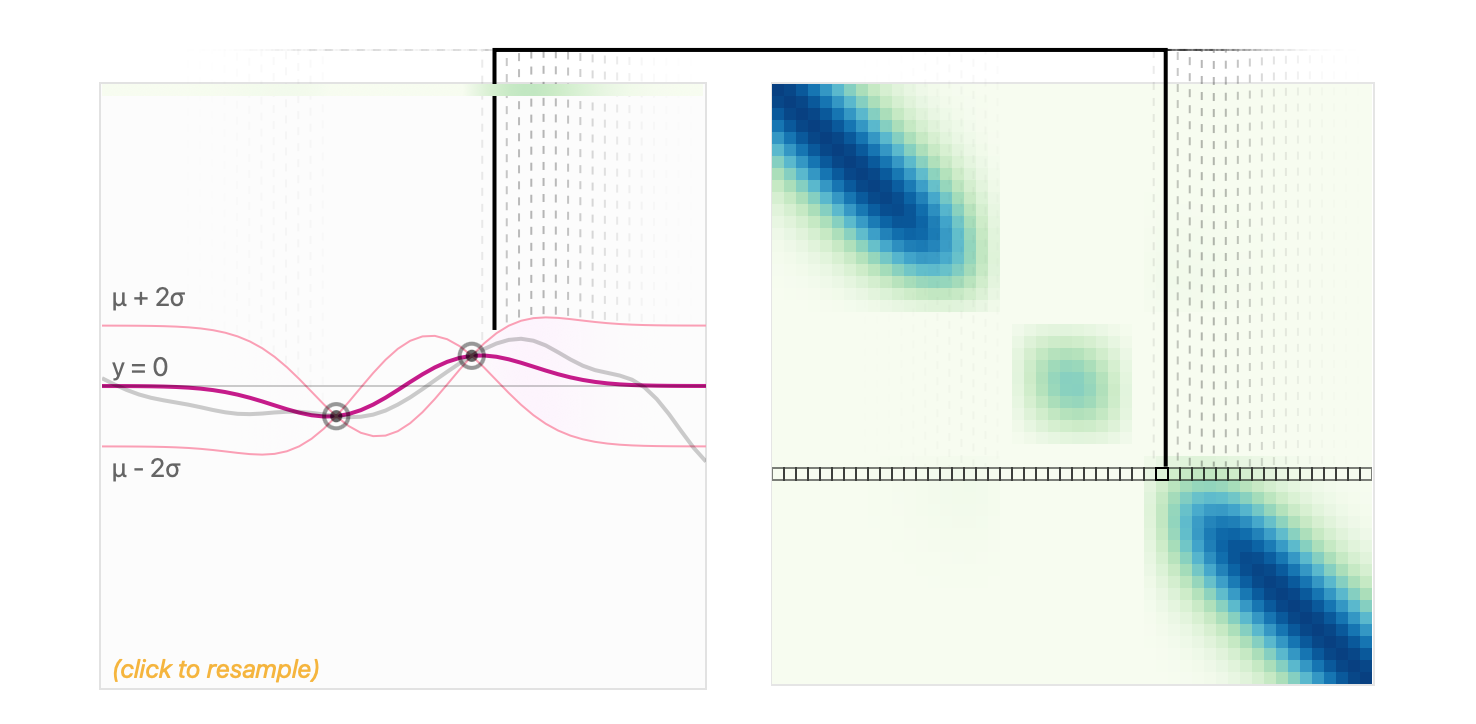
具体来讲对于观测点 $X$（训练点，注意这里的 $X$ 和上一小节的不同，这里是表示训练样本的特征）与其对应值 $Y$，所有的非观测点（测试点） $X^\ast$ 的值定义为 $f(X^\ast)$。 我们对预测值 $Y$ 构建多维高斯分布。 这里我们把均值向量替换为均值函数。 那么有，

$$\begin{bmatrix}Y\\f(X^\ast)\end{bmatrix}\sim N(\begin{bmatrix}\mu(X)\\\mu(X^\ast)\end{bmatrix}，\begin{bmatrix}k(X,X)& k(X,X^\ast)\\k(X^\ast,X)&k(X^\ast,X^\ast)\end{bmatrix})$$

同样的我们可以得到条件分布，

$$P(f(X^\ast)|Y,X^\ast,X) \sim N(\mu^\ast,k^\ast)$$

其中, $\mu^\ast=k(X^\ast,X)k(X,X)^{-1}(Y-\mu(X))+\mu(X^\ast)$，$k^\ast=k(X^\ast,X^\ast)-k(X^\ast,X)k(X,X)^{-1}k(X,X^\ast)$。 这个条件分布的含义是，在我们知道训练数据的特征以及标签和测试数据特征的情况下，我们可以得到测试数据的标签的分布。

一般在数据归一化的情况下，先验均值 $\mu(X)$ 和 $\mu(X^\ast)$ 可以设为 0 函数。 在 sklearn 中，可以通过调节参数 normalize_y=True 实现。 这样我们可以得到最终的高斯分布，即我们的预测输出。 其强相关于预测样本于训练样本的距离，训练样本的标签以及核函数的选择。