信息论以及机器学习中的熵

这里对机器学习中常用到的信息论知识点做一个总结。 第四次更新本文，每次都能发现之前的理解有疏漏和不清晰的地方。 这次更新本文为两部分，信息论中的熵 & 机器学习中的熵，主要包含相关的定义和何如理解这些概念。

信息论中的熵 – 编码的视角

信息编码

所谓信息编码，就是在信息传递时，进行的必要转化。 一般情况下，以比特传输信息。 为了使信息高效传播，高概率高频次传递的信息将以更短的编码展现，而较少发生的低概率信息编码则会更长，一个具体的例子是霍夫曼编码。 在这个背景下，某一个事件 $x$ 的编码长度则会与其概率 $p(x)$ 成负相关，一般来说至少需要 $\log _{2}\left({p(x)}\right)$ 个比特来对其进行编码。

信息熵

对于一个随机变量 $X$ 进行编码，考虑到每个事件 $x$ 出现的概率 $p(x)$ 和编码长度 $\log \left({p(x)}\right)$，对随机变量的编码可以由对每个事件编码的期望得到，这个期望就是信息熵：

$$H(X)=\mathbb{E}_{X}[I(x)]= - \sum_{x \in X} p(x) \log {p(x)}$$

在信息编码中，当我们用少于信息熵长度的比特编码时，一定有资讯的损失，所以信息熵被称为理论最优编码长度。 对于随机变量 $X$ 而言，信息熵是其不确定性的度量，也可以看作是信息量的期望：

• 当分布越平均，事件出现概率都相似，采样不确定性更大，杂乱信息多，信息熵越大。
• 当分布越不均，事件出现概率大不同，采样不确定性更小，杂乱信息少，信息熵越小。

交叉墒

我们已知每一个事件 $x$ 在一个已知的概率分布 $Q$ 下相应的编码长度为 $\log \left({q(x)}\right)$，当我们用这个编码对一个真实的（预先未知的）概率分布 $P$ 进行表示时，可以得到在这个新分布下期望的编码长度，这个期望就是交叉熵：

$$H(p, q)=-\sum_{x \in X} p(x) \log q(x)$$

说人话就是使用基于分布 $Q$ 的编码表来编码服从分布 $P$ 的样本所需的平均编码长度。 这个平均长度一定是不小于使用基于分布 $P$ 本身的编码表的，即$H(p, q) \geq H(p)$。

相对熵

对于分布 $P$ 和 $Q$，已知其交叉熵，可以得到 $P$ 相对于 $Q$ 的相对熵：

$$D_{\mathrm{KL}}(p \| q) = H(p, q) - H(p) =-\sum_{x} p(x) \log \frac{q(x)}{p(x)}$$

相对熵又称为 KL 散度，是两个概率分布 $P$ 和 $Q$ 差别的一种非对称性度量。 其表示使用基于分布 $Q$ 的编码表来编码服从分布 $P$ 的样本（相比起用 $P$ 自己的分布来编码）所需的额外的平均比特数。

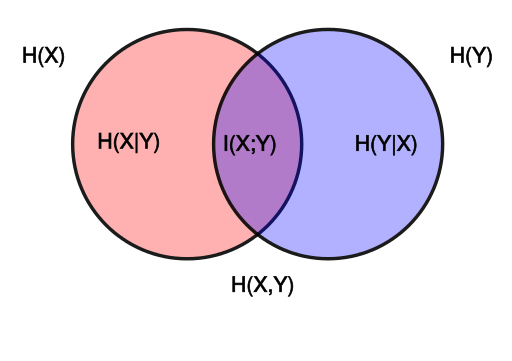
联合熵

Joint entropy，联合分布的熵。 那么对应的 $H(X)$ 和 $H(Y)$ 可被称作边缘熵。

$$H(X, Y)=\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log \left(\frac{1}{p(x, y)}\right)$$

条件熵

Conditional entropy，以条件概率计算的熵。

$$H(Y \mid X)=\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log \left(\frac{1}{p(y \mid x)}\right)$$

由贝叶斯定理 $p(x, y)=p(y \mid x) p(x)$ 可得条件熵和联合熵关系式：

$$H(X, Y)=H(X)+H(Y \mid X)=H(Y)+H(X \mid Y)=H(Y, X)$$

互信息

Mutual information 指两个集合之间的相关性，定义是随机变量 $(X,Y)$ 的联合分布与 $X$ 和 $Y$ 的边缘分布的乘积之间的差异，其具有对称性。

$$I(X ; Y)=D_{\mathrm{KL}}(p(x, y) \| p(x) \otimes p(y))$$

其可以理解为在获得一个随机变量的信息之后，观察另一个随机变量所获得的“信息量”（单位通常为比特）。 也可以理解为不确定性的减少量，即 $Y$ 中包含多少 $X$ 中的信息。

$$I(X ; Y)=H(X)-H(X \mid Y)=H(X)+H(Y)-H(X, Y)=H(Y)-H(Y \mid X)=I(Y ; X)$$

机器学习中的熵 – 应用与实现

作为损失函数使用的交叉墒

机器学习中，设计损失函数的思想就是考虑我们预测分布与真实分布的差异。 在这个情况下，相对熵是一个不错的选择。 同时由于相对熵中 $H(p)$ 是一个固定值并不重要，所以我们可以直接使用交叉熵作为神经网络的损失函数。 其形式为，

$$loss = -\sum_{i=1}^{n} y_i \log(\hat{y}_{i})$$

其中 $y_i$ 是第 $i$ 个样本的真实标记（参考 $p$ 来理解）。 $\hat{y}_{i}$ 是第 $i$ 个样本在不同类别上的概率，神经网络中这个概率常常使用 softmax 函数，或者 sigmoid 函数得到。

Pytorch 中实现

在 pytorch 中有两种方式实现交叉熵损失。 可以参考之前的这篇笔记。 可以调用NLLLoss()或CrossEntropyLoss()两个函数。 两函数的不同点主要在于输入不同：

• 最后一层全连接层的输出可以直接调用CrossEntropyLoss()
• 对于NLLLoss()，要将最后一层全连接层的输出再通过一次LogSoftmax()计算才能调用。

同时如果类别不平衡也可以在每一个类别上加上相应的权重。

交叉熵的求导

因为之前要的工作要手动计算损失函数反向传播时对最后一层参数的梯度，所以需要对交叉熵损失求导。 此处我们只需要考虑对最后一层全连接层的输出求导即可，对参数可以之后再进一步求导。

先考虑一下正向的过程（在 n 个类别下使用 softmax 的情况），对于一个样本在最后一层全连接层的输出 $X = [x_1,...,x_n]$，我们考虑第 $i$ 个类，

$$x_i \xrightarrow[i_{th} output]{LogSoftmax} - \ln (\frac{\exp (x_{i})}{\sum_{j=1}^{n} \exp (x_{j})}) \xrightarrow[]{Y} - y_i \ln (\frac{\exp (x_{i})}{\sum_{j=1}^{n} \exp (x_{j})})$$

当考虑所有类别时，一般是将最右端这一项加权平均或加权求和。 此处我们假设权重相等，对所有类别相加，则可以得到总损失。

$$loss = - \sum_{i=1}^{n}y_i \ln (\frac{\exp (x_{i})}{\sum_{j=1}^{n} \exp (x_{j})}) = - y_c \ln (\frac{\exp (x_{i})}{\sum_{j=1}^{n} \exp (x_{j})})$$

其中$y_c = 1$，指当前样本的真实标记是 $c$。

$$loss = - \ln (\frac{\exp (x_{c})}{\sum_{j=1}^{n} \exp (x_{j})}) = - \ln(Softmax(x_c)) = - \ln(S(x_c))$$

此处进行求导，

$$\frac{\partial loss}{\partial x_i} = - \frac{1}{S(x_c)} \frac{\partial S(x_c)}{\partial x_i}$$

而对于 softmax 函数求导需要分类讨论：

• 当$i=c$时, $\frac{\partial S(x_c)}{\partial x_i} = S(x_c)(1-S(x_c))$
• 当$i\neq c$时, $\frac{\partial S(x_c)}{\partial x_i} = - S(x_i)S(x_c)$

所以导数为：

• 当$i=c$时, $\frac{\partial loss}{\partial x_i} = S(x_i)-1$
• 当$i\neq c$时, $\frac{\partial loss}{\partial x_i} = S(x_i)-0$

Reference

• Cross entropy - From Wikipedia, the free encyclopedia
• Kullback–Leibler divergence - From Wikipedia, the free encyclopedia
• Information theory - From Wikipedia, the free encyclopedia
• Softmax以及Cross Entropy Loss求导
• 互信息
• Yu Zhang’s Blog