Boltzmann Machine

此处记录对于 Boltzmann Machine，即玻尔兹曼机的学习。 在互联网上并没有找到太多很好的资料，看了半天仍旧云里雾里，这里还是以我自己个人了解模型的思路来进行学习。 以目前的了解来看，这一系列模型用得并不太多，只是偶尔被拉出来提到，所以还是得看一下。

Restricted Boltzmann Machine 受限玻尔兹曼机

1. 模型长什么样子

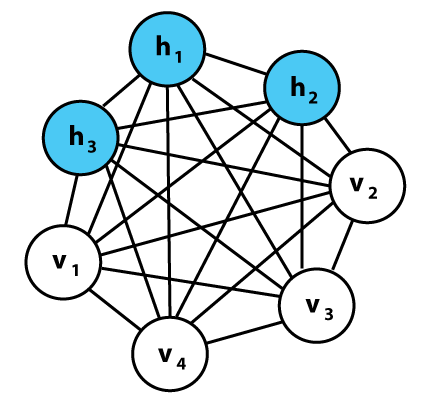
首先介绍玻尔兹曼机（BM），如图所示。 显而易见这是一个全连接的图，v 代表 visible 即可见节点，h 代表 hidden 即隐藏节点。

而对于受限玻尔兹曼机（RBM）而言，其包含可见层 V 和隐藏层 H，层内则不存在任何连接，即为一个二分图，如下所示。

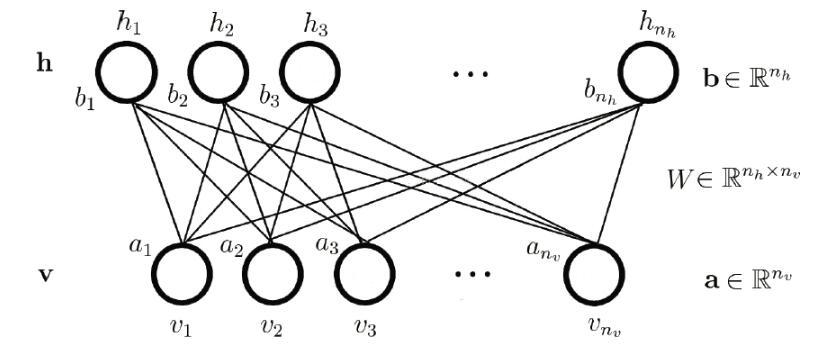
由于层内不存在连接，则当给定可见层神经元的状态时，各隐藏层神经元的激活条件独立；反之当给定隐藏层神经元的状态是，可见层神经元的激活也条件独立。

2. 模型如何做预测

在了解模型结构之后，我们需要知道假设我们已经有训练好的模型之后，如何进行预测。 换句话说就是预测需要用到模型中的那些部分以及需要进行什么步骤。

一般来说，我们做预测是想获得隐藏层（hidden）处的取值。 RBM中的每个神经元只可能是二元状态0或1中的一种。 我们最关心的因子是隐藏层或输入层地神经元位于状态1（激活）的概率。 给定一个输入向量 v，可以得出单个隐藏神经元 j 激活的概率：

$$p\left(h_j=1 \mid \mathbf{v}\right)=\frac{1}{1+e^{\left(-\left(b_j+W_j v_i\right)\right)}}=\sigma\left(b_j+\sum_i v_i w_{i j}\right)$$

同样的，给定一个隐藏层向量 j，可以得出单个输入神经元 i 激活的概率：

$$p\left(v_i=1 \mid \mathbf{h}\right)=\frac{1}{1+e^{\left(-\left(a_i+W_i h_j\right)\right)}}=\sigma\left(a_i+\sum_j h_j w_{i j}\right)$$

预先不知道的变量（或许通常为隐变量），即可作为模型的输出。

3. 模型如何训练

从模型的预测方式可以看出，在我们知道偏置向量和权值矩阵之后即可使用模型进行预测。 RBM 是一种基于能量的模型，它尝试最小化一个预先设定好的能量函数，在优化的过程中得到相关的参数。 首先这个能量定义为（至于为什么这样定义在此不做讨论）：

$$E(\mathbf{v}, \mathbf{h})=-\sum_i a_i v_i-\sum_j b_j h_j-\sum_{i, j} v_i h_j w_{i j}$$

然后可得其联合概率分布：

$$\begin{aligned} p(\mathbf{v}, \mathbf{h}) & =\frac{1}{Z} e^{-E(\mathbf{v}, \mathbf{h})} \\ Z & =\sum_{\mathbf{v}, \mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})} \end{aligned}$$

其中 Z 为配分函数（partition function），用来做归一化。 这个分布即为玻尔兹曼分布。 RBM 的训练包括为给定的输入值寻找使能量达到最小值的参数。 能量最小则联合分布最大，即当下状态的发生概率最大。

利用基于能量的模型的原因是这样的，对于一个给定的数据集，如果不知道其潜在的分布形式，那是非常难学习的，似然函数都写不出来。比如如果知道是高斯分布或者多项分布，那可以用最大化似然函数来学出需要学习的对应参数，但是如果分布的可能形式都不知道，这个方法就行不通。而统计力学的结论表明，任何概率分布都可以转变成基于能量的模型，所以利用基于能量的模型的这个形式，是一种学习概率分布的通法。

对于实际问题，我们可得观测数据的概率分布，即联合分布的一个边缘分布，即：

$$P_\theta(v)=\sum_h P_\theta(v, h)=\frac{1}{Z_\theta} \sum_h e^{-E_\theta(v, h)}$$

再使用最大似然估计（对数形式），在对应的样本集 S 上来求得对应的参数值。

$$\ln L_{\theta, S}=\ln \prod_{i=1}^{n_s} P\left(v^i\right)=\sum_{i=1}^{n_s} \ln P\left(v^i\right)$$

如何来计算梯度（以优化似然）呢？ 一般使用迭代的方式逼近。 目前在用的方法是吉布斯采样（得到原始向量重建值）+ 对比散度（使用重建值计算梯度）+ 梯度上升（更新梯度）的方法。 （具体细节在此不赘述，日后若有需要再深入学习。）

Deep Boltzmann Machine 和 Deep Belief Net

深度信念网络（DBN）也是经常听到的一个名词，其结构和深度玻尔兹曼机（DBM）有一些相似。 此处仅做一个了解，日后若有需要再深入学习。

模型长什么样子

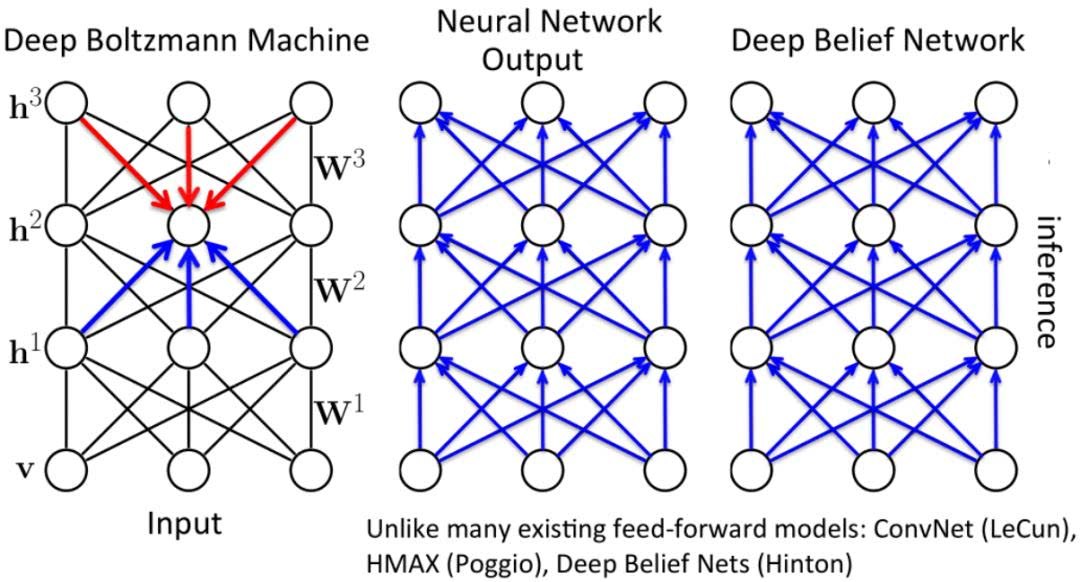
简单来说第一层都是一样的，即为一层 RBM。 DBN 的后面几层为前向网络，而 DBM 的后面几层仍为 RBM。 整体来看，DBN是有向图（除了最上层的RBM是无向图），是巧妙结合了有向图和无向图的生成模型；DBM每相邻的两层都是RBM，是完全的无向图。

Reference

• 受限玻尔兹曼机（RBM）学习笔记 - 祁昆仑的文章 - 知乎
• 深度学习邂逅物理：受限玻尔兹曼机原理解析
• 玻尔兹曼机
• 深度学习基础：Boltzmann Machines - 羽刻的文章 - 知乎
• 深度学习中，深度波尔兹曼机（DBM）和深度置信网络（DBN）都有哪些区别？ - gwave的回答 - 知乎
• 深度置信网络＆深度玻尔兹曼机