从 DETR 出发，目标检测再学习

目标检测是 CV 中的一个重要任务，其目标是在图像中找到物体的位置和类别。 当然，根据空间维度的不同，目标检测可以分为 2D 目标检测和 3D 目标检测。 本文聚焦于 2D 目标检测，主要介绍 DETR 这个基于 transformer 的目标检测模型。

目标检测任务

任务是什么？

目标检测任务，顾名思义，就是在图像中找到物体的位置和类别。 通常输入是一张图片，输出是一系列的 bounding box，每个 bounding box 包含一个物体的位置和类别。 用符号的语言来说：

• 输入：一张图片，可以表示为一个矩阵，维度为 $(H,W,C)$，其中 $H$ 为高度，$W$ 为宽度，$C$ 为通道数。
• 输出：一系列的 bounding box，每个 box 包含一个物体的位置和类别，可以表示为 $(x, y, w, h, c)$
  • 其中 $(x, y)$ 为 bounding box 的中心坐标，$(w, h)$ 为 bounding box 的宽度和高度，有时又可以转换表示为 $(x_{\text{min}}, y_{\text{min}}, x_{\text{max}}, y_{\text{max}})$
  • $c$ 为类别，通常为任务类别数加一（多一个背景类别）。

如何评估？

首先在我们的预测任务中，有若干个类别，每一个类别都有若干目标，每一个目标都有一个 bounding box。 我们的算法的输出是一个系列的 bounding box 以及某一个类别的置信度。 那么评估就需要对比预测和真值的差距。

一般来说，我们对每一个类别单独考虑。

• 首先，我们会使用 IoU（Intersection over Union）来评估两个 bounding box 的重叠程度。 IoU 的计算方式为 $\frac{\text{Area of Overlap}}{\text{Area of Union}}$，其值在 0 到 1 之间，越大表示重叠程度越高。 我们将预测结果按照该类的置信度排序，然后逐个计算 IoU，如果 IoU 大于某个重叠阈值（例如 0.5），我们认为这个预测是正确的。 （i.e.，如果我们模型认为某处有一定概率存在某物，这个位置的和真实标记重叠程度越大，那么预测就越正确。）
• 那么针对此排序，通过改变预测阈值，就可以计算一系列的 precision 和 recall。
  • 其中 precision 为 $\frac{\text{TP}}{\text{TP}+\text{FP}}$
  • recall 为 $\frac{\text{TP}}{\text{TP}+\text{FN}}$
• 这一系列的 precision 和 recall 可以绘制成曲线，称为 PR 曲线，其下方的面积称为 AP（Average Precision）。 需要注意的是，如果我们的预测框多于或少于真实框，那么就会出现 FP 或 FN，从而影响 precision 和 recall 的计算。
• 之后，我们可以计算所有类别的 AP 的平均值，称为 mAP（mean Average Precision）。

最终的 mAP 越高，说明我们的模型在目标检测任务上表现越好。

如何设计误差函数？

目标检测的误差函数通常是一个多任务学习的问题，其包含了两个部分：

• 位置误差：通常使用 L1 或者 L2 范数来计算，即预测的 bounding box 和真实的 bounding box 之间的差距。
• 分类误差：通常使用交叉熵来计算，即预测的类别和真实的类别之间的差距。

最终的误差函数是两者的加权和，即 $L=L_{\text{loc}}+\lambda L_{\text{cls}}$，其中 $\lambda$ 是一个超参数。

DETR 模型

DETR 是第一篇将 Transformer 应用到目标检测方向的算法。

模型结构

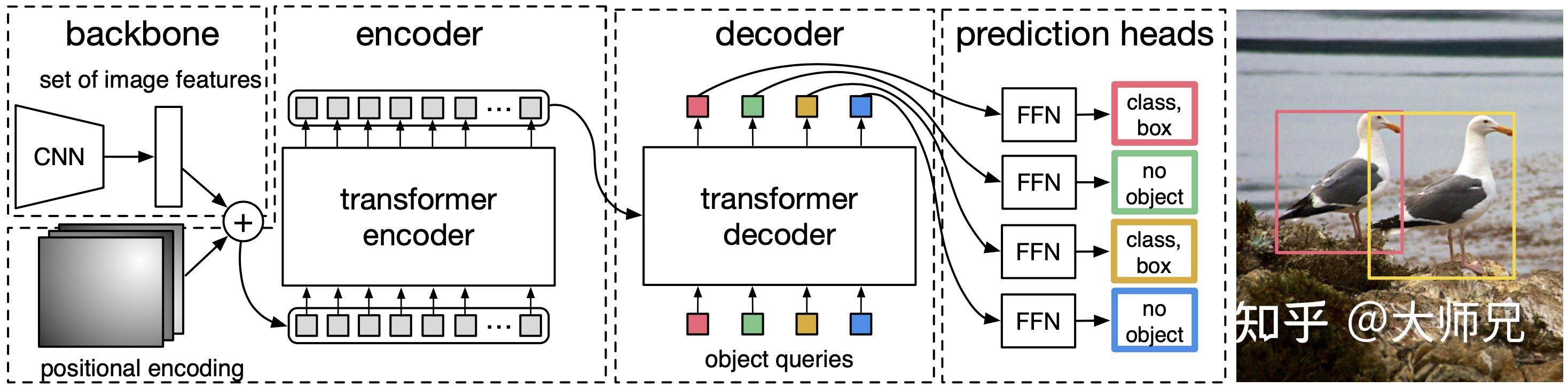
目标检测前向传导

• 首先原始图片通过骨干网络 CNN 提取特征，输入图片特征为 $x_{img} \in \mathbb{R}^{3 \times H' \times W'}$，输出为降采样 32 倍的特征 $f \in \mathbb{R}^{C \times H \times W}$，其中 $C$ 为通道数。
• 之后再通过一个卷积 $1 \times 1$ 降维，得到 $z \in \mathbb{R}^{d \times (H \times W)}$$，其中 $d$ 为一个更小的通道数。
• 之后将其加入位置编码（作为 Q 和 K），便可以作为编码器的输入。
• 解码器有两个输入，一个是编码器得到的特征，一个是 object queries，其维度为 $N \times d$，其中 $N$ 为目标的个数（一个事先设置好的超参数，通常远大于实际目标数）。
  • 初始层的 self-attention 中使用 object queries 作为 Q 和 K，V，其中
  • 中间层的多头 cross-attention 中使用编码器得到的特征作为 K 和 V，其中需要将位置编码加入 K。
  • Object queries 的作用类似于基于 CNN 的目标检测算法中的 anchor boxes，是一个可以训练的嵌入向量，用于预测目标的位置和类别。具体来说使用了 learnt positional encoding 作为 object queries，以保证每一个 query 可以独特的表示一个物体。
  • 原始的 object query 也会通过 skip connection 传入每一层解码器的自注意力模块中的 Q 和 K，以及交叉注意力模块中的 Q。
  • N 个结果不是顺序得到的，而是一次性得到 N 个结果，这点和原始的 Transformer 的自回归计算是不同的（只做一次输出）。
  • 每个 object queries 通过预测头预测目标的 bounding box 和类别，其中 bounding box 有三个值，分别是目标的中心点以及宽和高。超过目标个数的 ground truth 使用背景元素来作为负样本。

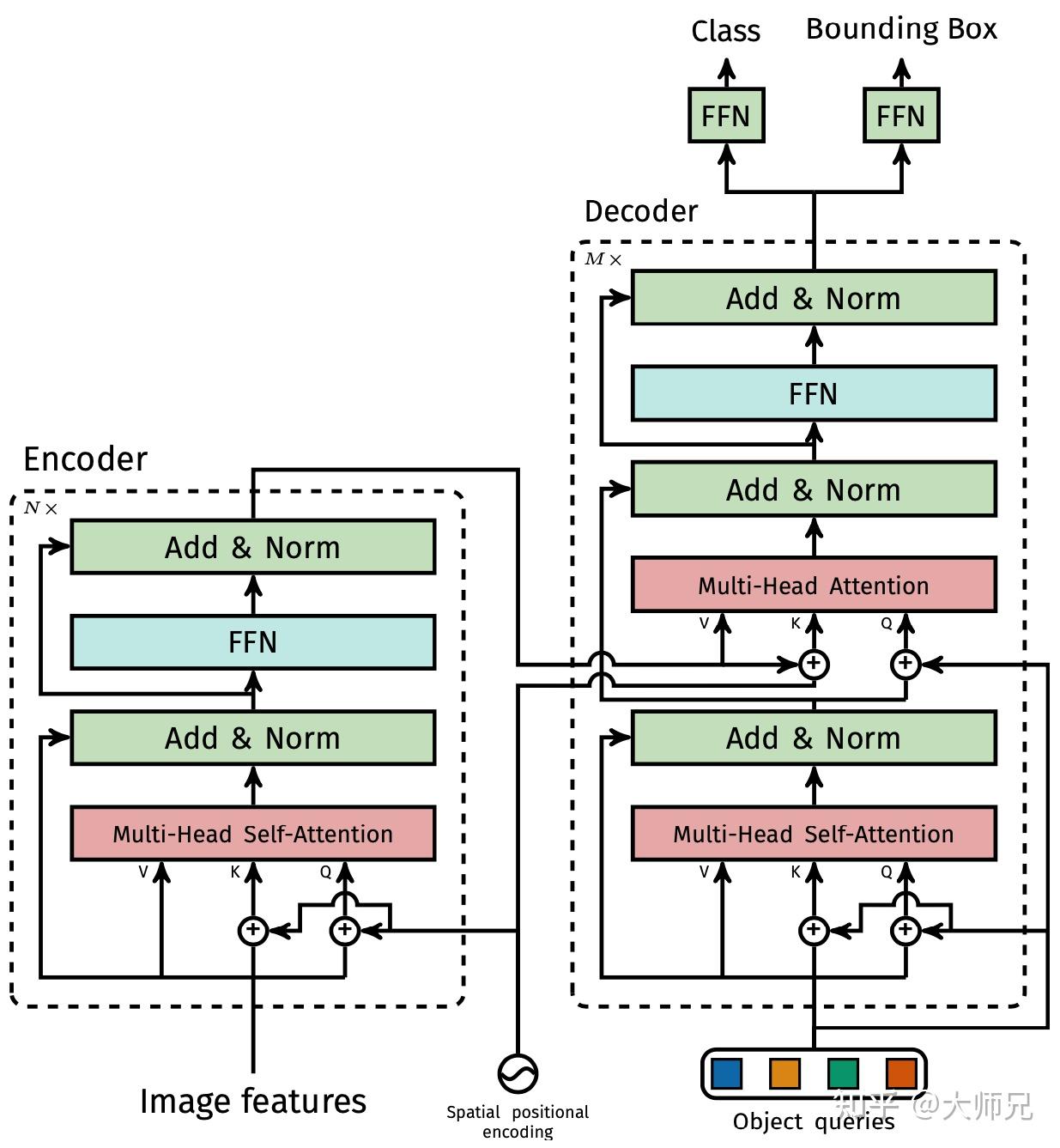
目标检测损失计算

得到预测结果以后，将 object predictions 和 ground truth box 之间通过匈牙利算法进行二分匹配。 注意，匈牙利算法是用于解决二分图匹配的问题，即将 ground truth 的 K 个 bbox 和预测出的 100 个 bbox 作为二分图的两个集合，匈牙利算法的目标就是找到最大匹配，即在二分图中最多能找到多少条没有公共端点的边。匈牙利算法的输入就是每条边的 cost 矩阵 假如有 K 个目标，那么 100 个 object predictions 中就会有 K 个能够匹配到这 K 个 ground truth，其他的都会和 “no object” 匹配成功，使其在理论上每个 object query 都有唯一匹配的目标，不会存在重叠。

Bounding box 和 ground truth 的匹配代价表示为:

$$\mathcal{L}_{\text {match }}=-1_{\left\{c_i \neq \varnothing\right\}} \hat{p}_{\sigma(i)}\left(c_i\right)+1_{\left\{c_i \neq \varnothing\right\}} \mathcal{L}_{\text {box }}\left(b_i, \hat{b}_{\sigma(i)}\right)$$

其中 $1_{\left\{c_i \neq \varnothing\right\}}$ 是一个 bool 函数，当 $c_i \neq \varnothing$ 时为 1 ，否则为 0 。 $c_i$ 是第 $i$ 个物体的类别标签。 $\sigma(i)$ 是与第 $i$ 个目标匹配的 bounding box 的 index。 $\hat{p}_{\sigma(i)}\left(c_i\right)$ 表示DETR预测的第 $\sigma(i)$ 个预测的 bounding box 的类别为 $c_i$ 的概率。 $b_i$ 和 $\hat{b}_i$ 分别是第 $i$ 个目标的位置的ground truth的坐标 （中心点，宽，高）和预测的 bounding box 的坐标。 $\mathcal{L}_{\text {box }}$ 是两个矩形框之间的距离，下面我们详细介绍它。 $\mathcal{L}_{\text {box }}$ 由 loU 损失和 L1 损失构成，它们通过 $\lambda_{\text {iou }}$ 和 $\lambda_{\mathrm{L} 1}$ 来控制两个损失的权值，表示为：

$$\mathcal{L}_{\text {box }}\left(b_{\sigma(i)}, \hat{b}_i\right)=\lambda_{\text {iou }} \mathcal{L}_{\text {iou }}\left(b_{\sigma(i)}, \hat{b}_i\right)+\lambda_{\mathrm{L} 1}\left\|b_{\sigma(i)}-\hat{b}_i\right\|_1$$

其中 $\mathcal{L}_{\text {iou }}$ 使用的是 GloU 损失，考虑了两个检测框最小外接矩形的大小（反应两者如何相交），表示为：

$$\mathcal{L}_{\text {iou }}\left(b_{\sigma(i)}, \hat{b}_i\right)=1-\left(\frac{\left|b_{\sigma(i)} \cap \hat{b}_i\right|}{\left|b_{\sigma(i)} \cup \hat{b}_i\right|}-\frac{\left|B\left(b_{\sigma(i)}, \hat{b}_i\right) \backslash b_{\sigma(i)} \cup \hat{b}_i\right|}{\left|B\left(b_{\sigma(i)}, \hat{b}_i\right)\right|}\right)$$

当我们通过上面的策略得到 ground truth 和预测 bounding box 的最优二部图匹配后，便可以根据匹配的结果计算损失函数了。 DETR 的损失函数和匹配代价非常类似，不同的是它的类别预测使用的是对数似然，表示为式。

$$\mathcal{L}_{\text {Hungarian}}(y, \hat{y})=\sum_{i=1}^N\left[-\log \hat{p}_{\hat{\sigma}(i)}\left(c_i\right)+1_{\left\{c_i \neq \varnothing\right\}} \mathcal{L}_{\text {box }}\left(b_i, \hat{b}_{\hat{\sigma}}(i)\right)\right]$$

它们另外一个不同是 bool 函数作用的位置不同，在 $\mathcal{L}_{\text {match}}$ 中背景目标不参与匹配代价的计算， $\mathcal{L}_{\text {Hungarian}}$ 则也要计算背景目标的分类损失。

全景分割前向传导

全景分割是继语义分割和实例分割之后的另一个更难的分割任务，它需要给图像中的每个像素点分配一个语义标签和一个实例 id。 其中语义标签是物体的类别，实例 id 是每个不同物体对应的编号。

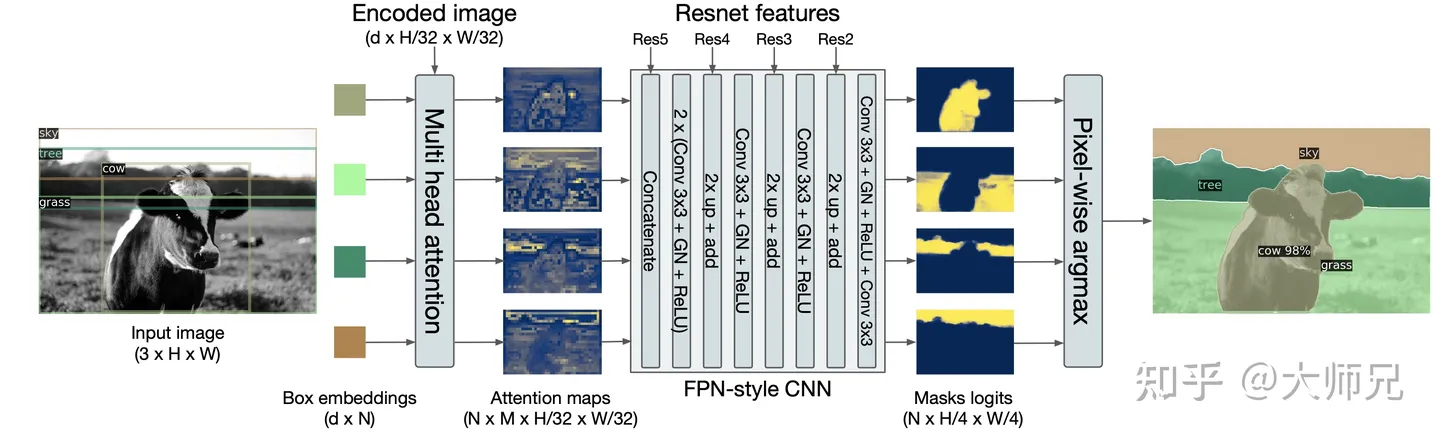
在 DETR 中，它将全景分割任务分成 N 个在每个 bounding box 上的两个类别的分割任务，相比于目标检测，主要的区别在于模型的输出头。 首先通过 CNN（残差网络）将图像编码降采样的 Feature Map，然后通过一组多头自注意力将 Feature Map 和 bounding box 的位置编码信息作为输入得到 N 个小尺寸的Attention Maps（类似之前的步骤）。 再通过一组类似 FPN 的架构将图像上采样的原图的 1/4，得到 N 个mask logits，最后通过按像素点取 softmax 得到最终的分割效果。

全景分割损失计算

骰子损失（DICE Loss）是在 V-Net 中提出的类似于 loU 损失的专门用于分割任务的损失函数，它的主要应用场景是分割任务中类别不平衡的问题。 DICE 损失来自于 DICE 系数（DICE coefficient），它是一个集合相似度的衡量函数, 通常用来计算两个样本的相似度。

DETR的分割任务使用的损失函数表示为,

$$\mathcal{L}_{\text {DICE }}(m, \hat{m})=1-\frac{2 m \sigma(\hat{m})+1}{\sigma(\hat{m})+m+1}$$

其中 $\sigma$ 是 sigmoid 激活函数。 此项损失可以理解为某种 IoU，即预测的 mask 和真实的 mask 之间的重叠程度。 此项损失会根据目标数进行归一化。

总结

本文是一个完整的目标检测任务及 DETR 模型介绍。 之后的很多 2/3D 目标检测工作都是在此模型基础上进行的。 基于 transformer 的目标检测模型是值得深入研究的方向。

Reference

1. mean Average Precision (mAP)
2. Transformer目标检测之DETR
3. Carion, Nicolas, et al. “End-to-end object detection with transformers.” European conference on computer vision. Cham: Springer International Publishing, 2020.