人工智能中的逻辑

将逻辑作为基于知识的 Agent 的一类通用表示，这样的 Agent 通过对信息的组合和再组合以适应各种用途。 本文一部分参考了这位同学的笔记。

Logics: formal languages for representing knowledge to extract conclusions

基于知识的 Agent

• 知识库（KB）：基于知识的 Agent 的核心部件。是一个“语句”集合。
• 语句（sentence）：用知识表示语言表达，表示了关于世界的某些断言。
• 公理：当某语句是直接给定而不是推导得到的时候，我们将其称为公理。

每次调用 Agent 程序，他做三件事：

1. Agent TELL 知识库他所感知到的内容。
2. Agent ASK 知识库应该执行什么行动。
   • 在此过程中可能会对于世界的当前状态，可能行动队列进行大量推理。
3. Agent TELL 知识库他采取的行动，并执行该行动。

逻辑知识与概念

逻辑：一种形式语言，可以表示能得出结论的信息

• 语法（Syntax）：定义了语言中的句子
• 语义（Semantics）：定义了句子的意思，即语义定义了每个语句关于每个可能世界的真值

蕴涵（Entailment）

• 蕴涵意为一个语句逻辑上跟随另一个语句而出现：$KB |= \alpha$
• 知识库 KB 蕴涵句子 $\alpha$ 当且仅当在 KB 为真的每个世界中，$\alpha$也为真
• 蕴涵是句子间的关系，其基于语义。
• 例如，x=0 蕴含 xy=0。

逻辑推理（inference）：

• 如果推理算法 i 可以根据 KB 导出 $\alpha$，我们表示为：$KB |-_{i} \alpha$，读为“i 从 KB 导出 $\alpha$”
• KB的所有推论集合是一个干草堆，α是针，蕴含=干草堆里的针，推理=找到它
• 对于推理算法 i：
  • 可靠性 Sound：不会虚构事实，只导出语义蕴涵句。
  • 完备性 Completeness：可以生成任一蕴涵句。

命题逻辑

Syntax 语法：

• 原子语句：命题符号P1，P2等是句子，代表一个或为真或为假的命题
• 复合句：
  • 如果S是一个句子，则┐S也是一个句子（negation 非，否定式）
  • 如果S1和S2是句子，则S1∧S2是句子（conjunction 与，合取式）
  • 如果S1和S2是句子，则S1∨S2是句子（disjunction 或，析取式）
  • 如果S1和S2是句子，则S1=>S2是句子（implication 蕴涵，蕴涵式）
  • 如果S1和S2是句子，则S1<=>S2是句子（biconditional 当且仅当，双向蕴涵式）

语义：

• 定义了判定特定模型中语句真值的规则。
• 可以用真值表总结

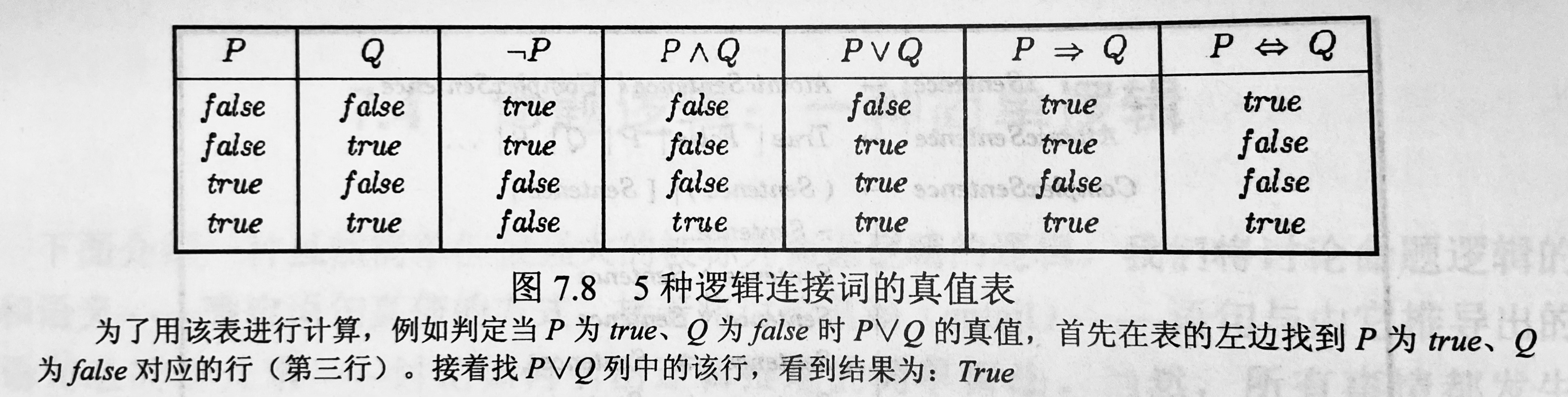
其中=>的真值表比较令人困惑。

• 不要用如果 P 那么 Q的思路来理解。
  • 命题逻辑不要求 P/Q 间的相关性或因果关系。
• 以“如果 P 为真，那我主张 Q 为真，否则无可奉告”来理解。
  • 前提为假的任意蕴含都为真。
  • 该语句为假的唯一条件是 P 为真而 Q 为假。

算符具有一定的运算性质（逻辑等价）：

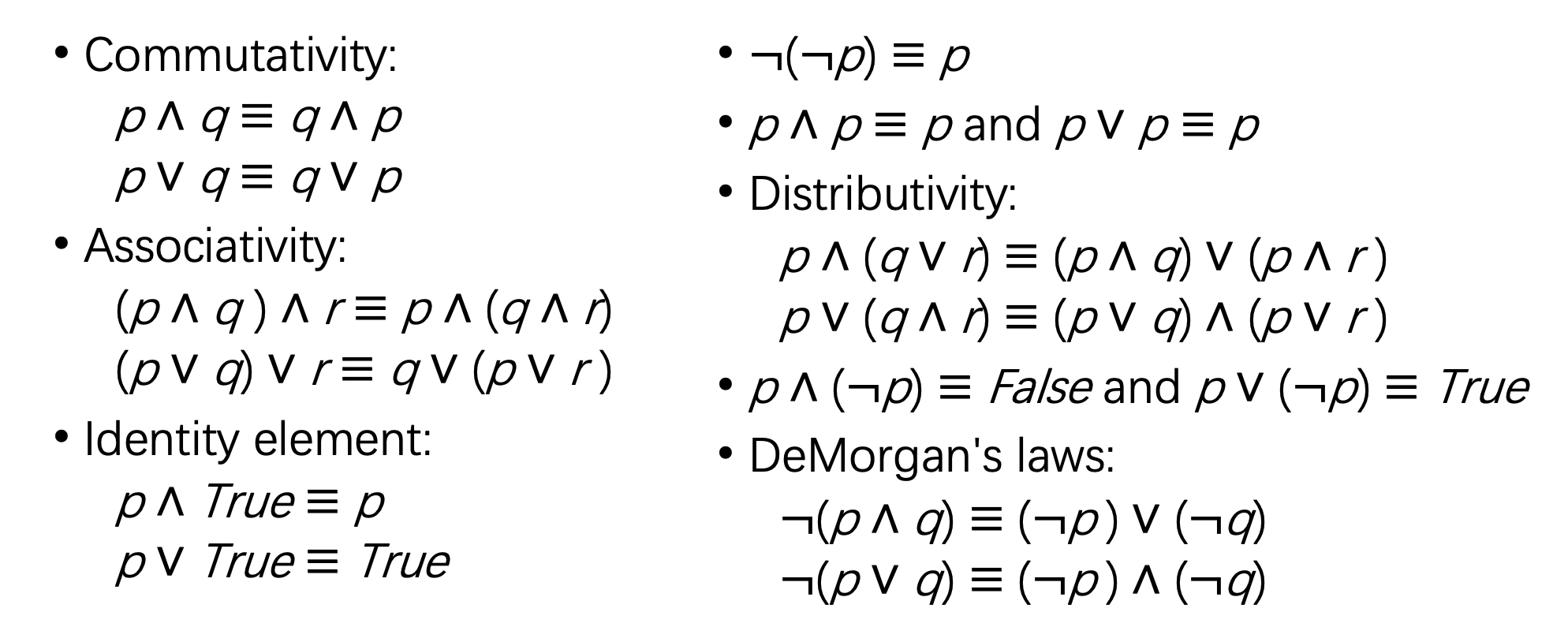
Implication 的几形式变换，真值可能会发生变换：

推导和证明

下列表示意为，给定任何形式的上方语句，就可以推导出下方语句：

• Modus Ponens: 假言推理原则 $\frac{\alpha \Rightarrow \beta, \quad \alpha}{\beta}$
• Modus Tollens: 假言推理原则 $\frac{\alpha \Rightarrow \beta, \quad \neg \beta}{\neg \alpha}$
• Addition: $\frac{\alpha}{\alpha \vee \beta}$
• Simplification/And-Elimination: $\frac{\alpha \wedge \beta}{\beta}$
• Disjunctive-syllogism: $\frac{\alpha \vee \beta, \quad \neg \alpha}{\beta}$
• Hypothetical-syllogism: $\frac{\alpha \Rightarrow \beta, \quad \beta \Rightarrow \gamma}{\alpha \Rightarrow \gamma}$

Search for proofs is a more efficient way than enumerating models:

• Truth tables have an exponential number of models.
• The idea of inference is to repeat applying inference rules to the KB.
• Inference is sound, but how about completeness?

如何来保证完备性？

• Proof by resolution
• Forward or Backward chaining

归结（Resolution）

类似于 Disjunctive-syllogism。 如果两个中必存在一个，而又不是第一个，则是第二个。

单元归结（Unit resolution）

$$\frac{\ell_{1} \vee \cdots \vee \ell_{k} \quad m}{\ell_{1} \vee \cdots \vee \ell_{i-1} \vee \ell_{i+1} \vee \cdots \vee \ell_{k}}$$

全归结（Full resolution）

$$\frac{\ell_{1} \vee \cdots \vee \ell_{k} \quad m_{1} \vee \cdots \vee m_{n}}{\ell_{1} \vee \cdots \vee \ell_{i-1} \vee \ell_{i+1} \vee \cdots \vee \ell_{k} \vee m_{1} \vee \cdots \vee m_{j-1} \vee m_{j+1} \vee \cdots \vee m_{n}}$$

其中 $\ell_{i}$ 和 $m_{j}$ 是互补文字。

合取范式（CNF）

以子句的合取式表达的语句被称为合取范式或者 CNF， 合取式不易阅读，但其将成为归结过程的输入：

• 消去等价词
• 消去蕴含次
• 否定词只出现在文字前边（而不是括号前面）

归结算法

为了证明 $KB |= \alpha$，需要证明 $(KB \wedge \neg\alpha)$是不可满足的，通过推倒矛盾来证明。

• 先将 $(KB \wedge \neg\alpha)$ 转化为 CNF。
• 对子句运用归结规则，产生新子句，如果其尚未出现过，则将其加入子句集，直到：
  • 没有可以添加的新语句。
  • 两个子句归结出空子句，等价于 False。（函数返回 True）

基本归结定理：如果子句集是不可满足的，那么这些子句的归结闭包包含空子句。

Forward or Backward chaining

前向链接 Forward Chaining：

• 判断单个命题词是否被限定子句的知识库所蕴含。
• 这个算法运行的时间是线性的。
• data-driven

反向链接 Backward Chaining：

• 从查询开始进行推理，如果查询为真则停止，否则，从知识库寻找以 q 为结论的蕴含式，如果前提都为真，则为真。
• 这个算法运行的时间也是线性的。
• goal-driven

DPLL Algorithm

• Check the satisfiablity of a sentence in propositional logic.
• 类似 backtracking 但是运用了很多启发式的技术，例如早停、纯符号启发式、单元子句启发式等。

一阶逻辑 First Order Logic（FOL）

可以作为 Propositional Logic 的替代。 （命题逻辑表达能力很弱。）

总结 Summary