约束满足问题（CSPs）

人工智能中的约束满足问题（Constraint Satisfaction Problems 问题）学习笔记。

约束满足问题

约束满足问题的目标是在一定的约束下，寻找符合条件的状态。 这种问题在生活中比较常见，以大学排课为例，已知教授的授课可以授课的时间，寻求满足所有教授时间的排课课程表。 常见的一些约束满足问题有：

• 八皇后问题
• 图着色问题
• 填字游戏
• 数独

问题定义

CSPs 包含以下三个要素：

• A set of variables（变量）, $X=\{X_{1},\ldots ,X_{n}\}$
• A set of domains （值域） for each variable: $D=\{D_{1},\ldots ,D_{n}\}$
• A set of constraints $C=\{C_{1},\ldots ,C_{m}\}$ （限制条件） that specify allowable combinations of values. Every constraint $C_{j}\in C$ is in turn a pair $\langle t_{j},R_{j}\rangle$ , where $t_{j}\subset X$ is a subset of k variables and $R_{j}$ is a k-ary relation (among k variables) on the corresponding subset of domains $D_{j}$.

问题的状态由对部分或者全部变量的定值（assignment）来确定：

• 如果定值不违反任何的限制条件，我们说他是无矛盾的（consistent）
• 如果定值包含了所有的变数，我们说他是完备的（complete）
• 如果定值是无矛盾的且完备的，我们说这个定值是一个解（solution），这样的定值就是 CSP 的解。

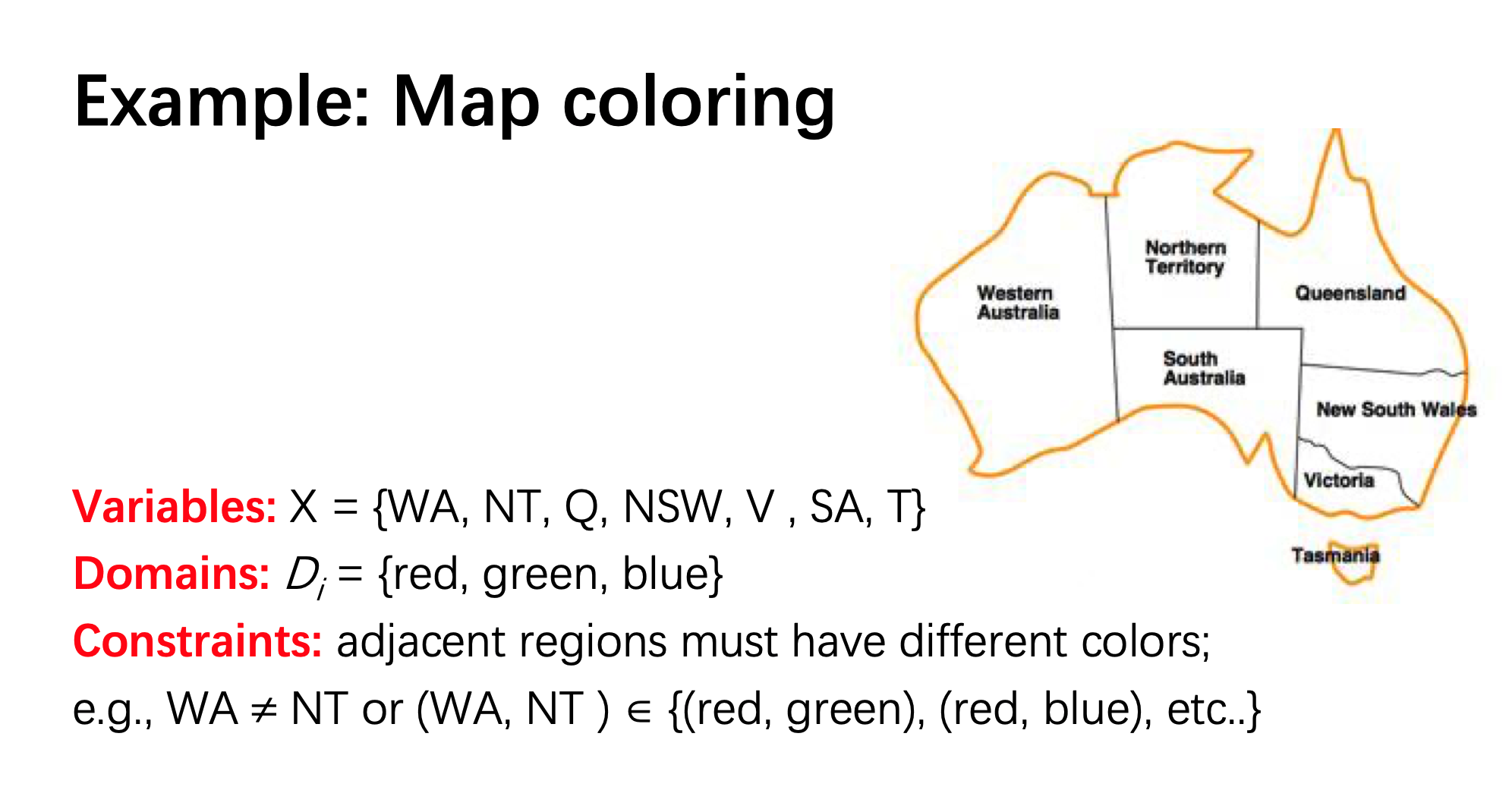
一个图着色问题的例子：

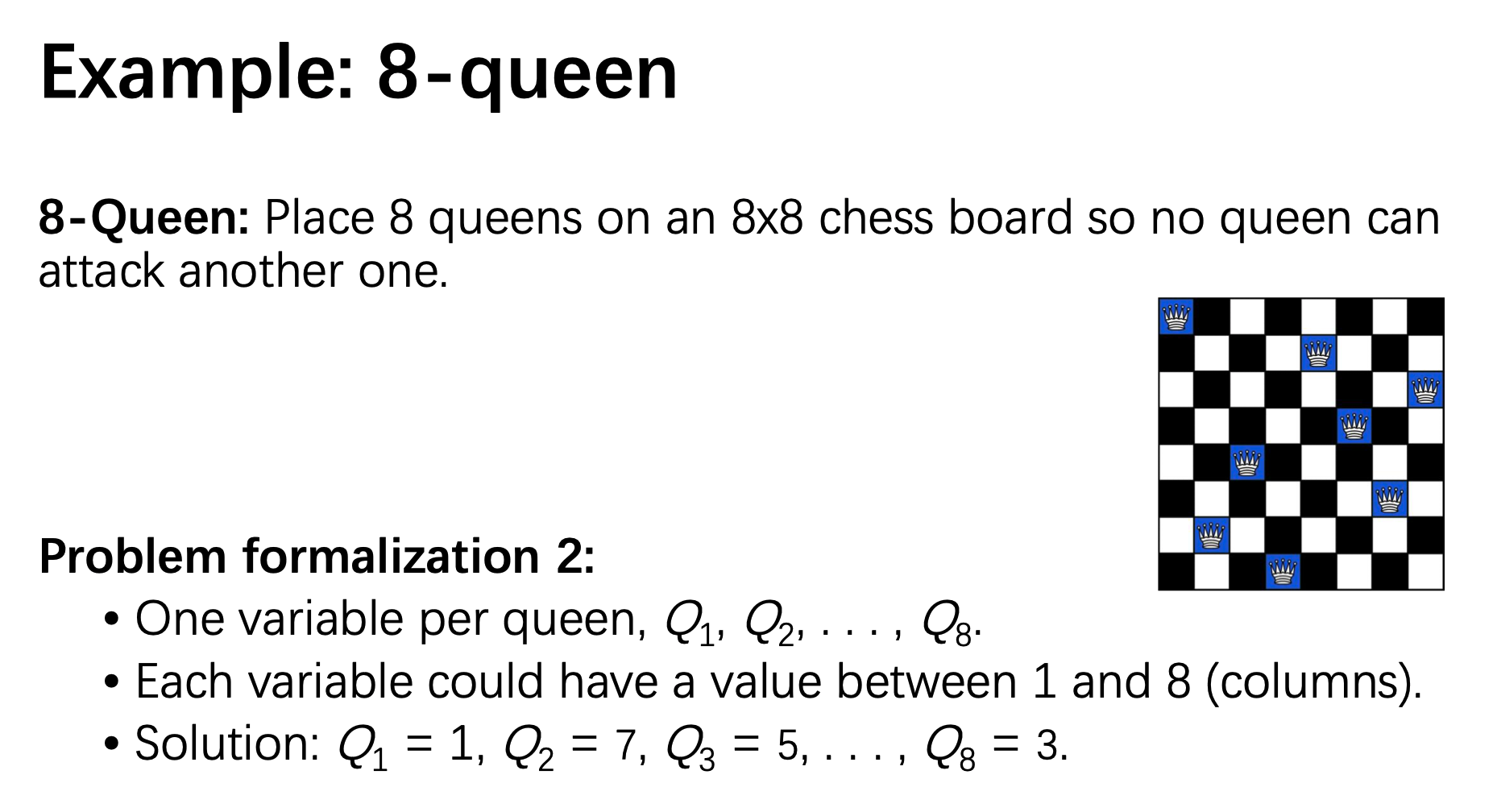
一个八皇后问题的例子：

一般来说 CSPs 使用的都是绝对约束，如果是非绝对的约束（偏好性），这样的问题称为约束优化问题（COP），在此不做讨论。

求解 CSPs

CSPs 形式化的优点

1. 快速消减庞大的搜索空间
2. 发现某部分不是解迅速丢弃，直观看到哪一部分变量赋值违反约束。
3. CSP 具有可交换性（commutative）

CSPs 中的局部相容性（consistency）

在 CSPs 中，算法可以搜索，也可以做一种称作约束传播的推理。 推理的目的是用约束减小一个变量的合法取值范围。 可以把推理作为搜索前的预处理步骤。 核心思想是增强局部相容性，使不相容的结点取值被删除。

• 节点相容（Node-consistency）：来自节点本身的一元约束
• 弧相容（Arc-consistency）：某变量所有取值满足该变量所有的二元约束。
  • 最流行的算法是 AC-3，维护一个弧相容队列。
    • 从队列弹出一条弧，使其一个节点弧相容，如果其值域无变化，则处理下一条弧。
    • 如果其值域发生变化，那么每个指向这个节点的弧必须重新插入队列准备检验。
• 路径相容（Path-consistency）：通过观察变量得到隐式约束并以此来加强二元约束。
  • 比如说有三个连接节点，却只有两种颜色。
  • 所有的 n-ary 约束都可以转换为 binary 约束。

具体解法：回溯搜索

仍然使用搜索来求解，一般来说使用 Backtracking Search（BTS）回溯搜索。 用于深度优先之中，每次为一个变量选择一个赋值，当没有合法的值时就回溯。 由于可交换性，我们只用搜索组合而不是排列，所以叶节点个数至多为$d^n$个（不回溯的情况）。

在回溯搜索中，也需要考虑如下问题来对搜索进行改进：

• 下一步给哪个变量赋值？对于所选变量，选用怎样的赋值顺序？
• 每步搜索应该进行怎样的推理？是否能预见失败？
• 当我们搜索到某赋值违反约束时，搜索本身能避免重复这样的失败吗？

1. 下一步给哪个变量赋值？对于所选变量，选用怎样的赋值顺序？

选取变量：

• 最少剩余值启发式 Minimum Remaining Value (MRV)，选择合法取值最少的变量赋值。这样通过早期有效剪枝有助于最小化节点数。
• 对于第一个节点而言，最小剩余值相同，应该选用度启发式，选择与其他未赋值变量约束最多的变量来试图降低未来的分支因子。

选取赋值：

• 最小约束值 Least Constraining Value (LCV)，试图为剩余变量赋值留下最大的空间。这里只需要找到一个解，所以优先考虑最可能的值。

2. 每步搜索应该进行怎样的推理？是否能预见失败？

搜索和推理应当交替进行。 推理的目的是减小值域，减小搜索空间。 当我们决定给某个变量某个值时，都有机会推理其邻接变量的值域空间。

• 最简单的形式是向前检验 Forward Checking（FC）。跟踪维护所有为选取变量的可能取值，当任何一个变量没有合法取值时结束。联合使用 MRV 和前向检验，很多问题的搜索将更有效。但是前向检验只使当前变量弧相容，却不向前看使其他变量弧相容。
• MAC 维护弧相容，递归传播约束。对一个变量赋值后，使用 AC-3，从临接的未赋值变量开始进行约束传播，如果值域为空，则调用失败立即回溯。

3. 当我们搜索到某赋值违反约束时，搜索本身能避免重复这样的失败吗？

• 简单的时序回溯。退回到上一个变量
• 冲突指导的回溯。退回到可能解决当前问题的变量（因为上一个变量可能无力于解决当前冲突）。构建一个冲突集，回溯到冲突集中时间最近的赋值。