对抗搜索问题和 Minimax 算法

人工智能中的对抗搜索学习笔记。

对抗搜索问题

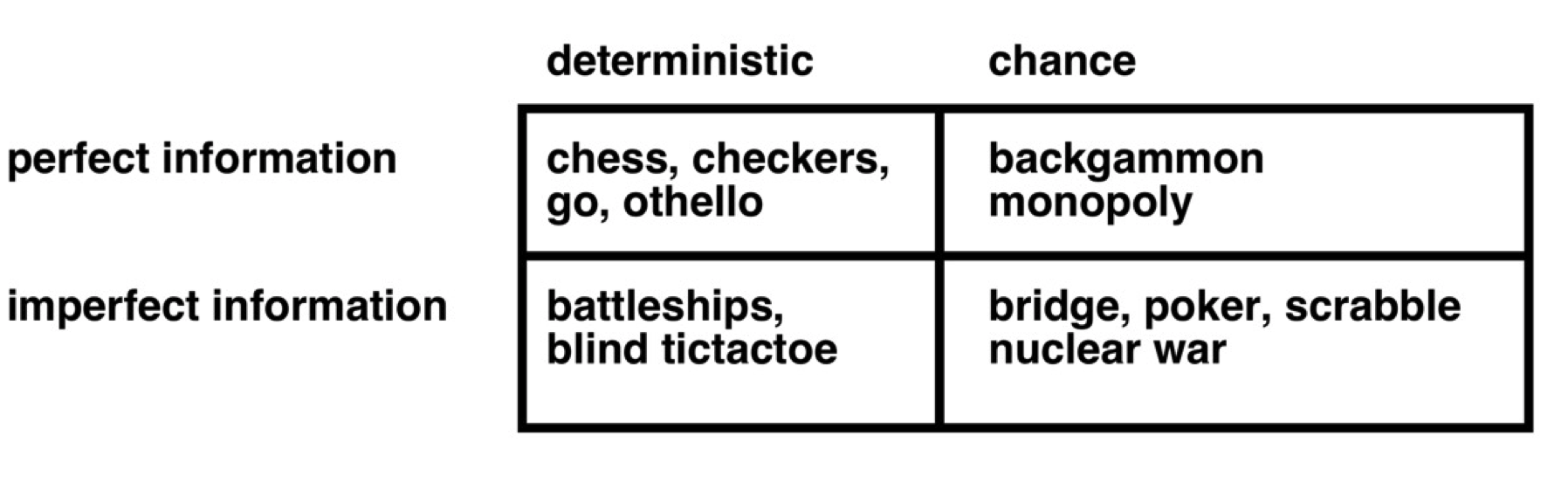
对抗搜索其实可以看作游戏场景，存在一个我们不能控制的对手。 相比于搜索，我们不是要找一个值或一系列序列，而是要找一个策略（strategy/policy）来对对手的行为进行反馈。 而游戏是人工智能中一个比较难的方向，它可以分为以下几类。

正式化 Formalization

将对抗搜索的问题抽象化，正式化，我们会得到以下要素：

• $s$: state, $s \in S$.
• $p$: $p \in P(s)$, defines which player has the move in state $s$. Usually taking turns.
• $a$: action, $a \in A(s)$, returns the set of legal moves in $s$.
• $T(s,a)$: $S \times A \rightarrow S$, transition function, defines the result of a move.
• $u(s,p)$: utility function or objective function for a game that ends in terminal state s for player p. It describes the earning at the end of the game.
• $\pi(s): S \rightarrow A$, strategy, output an action given a state.

Minimax 算法

这里很多内容参考了 Yu Zhang 的笔记。

问题背景

这里不再是广义的游戏背景，一般来说做出了一些限制。 Minimax 算法常用于**「有限状态，零和，完全信息，两个玩家（Max/Min）」**博弈问题，比如棋类。

算法概要

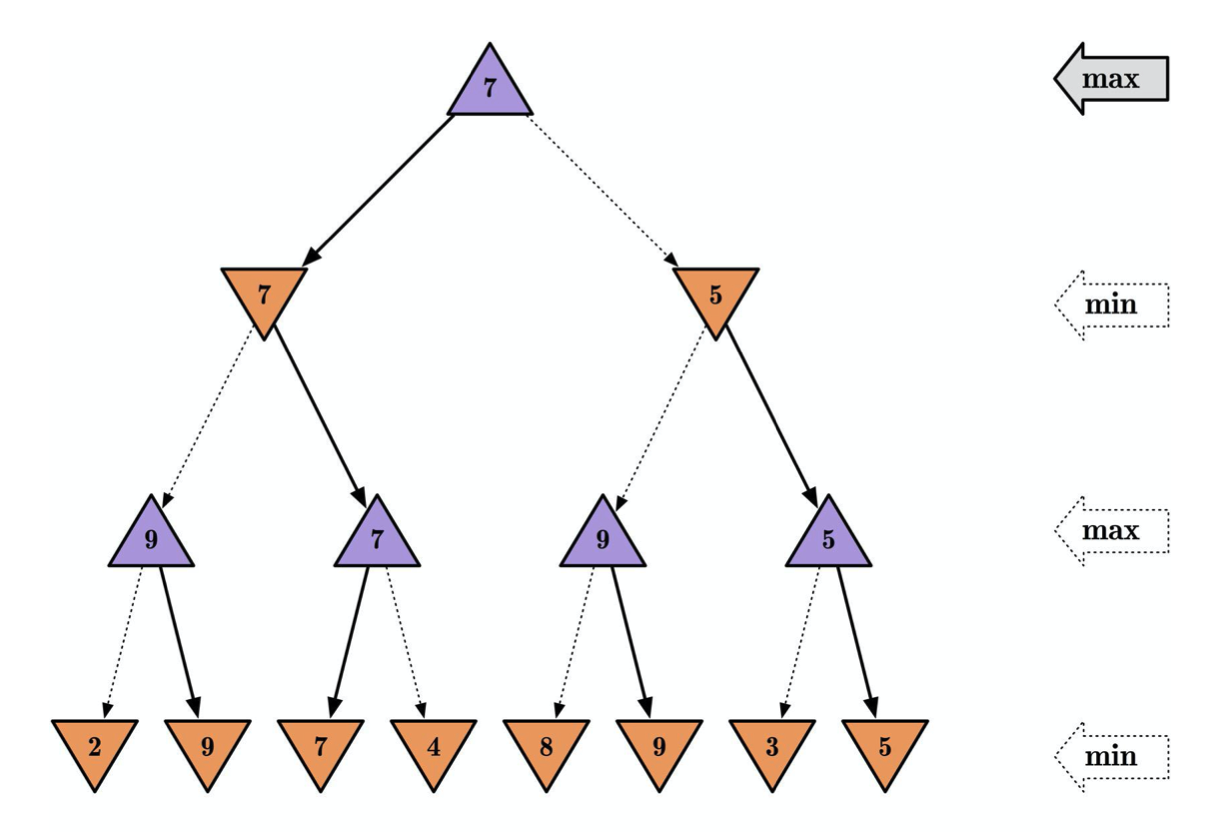
存在两个玩家，Max（希望最大化自己的收益），Min（希望最小化 Max 的收益）。 从初始状态开始，通过两个玩家选用不同动作交替操作，可以形成一个树，树中的每一个节点都代表一个状态$s$。 我们的目标是找到一个给 Max 的最优策略，使在游戏结束时的状态拥有最大的效用函数，这是一个在树中搜索的问题。

在 minimax 算法中，我们认为每一个状态 $s$ 都拥有一个 minimax 值（递归得到）。 这个值表示从当前状态 s 开始，双方均采取最优策略直至游戏结束时玩家 Max 的效用值 具体到计算过程中，如果状态为终止状态，那么它就是当下的效用值；如果是中间状态，则是子状态 minimax 值中的（最大值，Max 操作，目的最有利于自己；最小值，Min 操作，目的最不利于 Max）：

$$\text{minimax}(s)= \left\{ \begin{aligned} &u(s, \text{Max}) & & \text{if GameOver}(s) \\ &\max_{a \in A(s)}\text{minimax}(T(s,a)) & & \text{if Max's turn}\\ &\min_{a \in A(s)}\text{minimax}(T(s,a)) & & \text{if Min's turn} \end{aligned} \right.$$

对于算法的解释

• 对于游戏树的 DFS 搜索，从终点回推过程节点的 minimax 值。
• 最优/最终的节点可以出现于任何深度。
• 在 Max 使用最优策略的情况下：
  • 如果对手 Min 使用最优策略，那么一个节点只要计算出了 minimax 值，就已经看到了游戏的结局（效用值）。
  • 如果对手 Min 不使用最优策略，那么 Max 的最终效用只会更高。

一个简单的例子，自下而上的递归推导。

Alpha-Beta 剪枝

假设 game tree 的深度为 $m$，每个节点有 $b$ 种走法，则该算法的时间复杂度为$O(b^m)$，在实际情况中是不现实的。 相应的，其空间复杂度为$O(bm)$。 哪怕是在最简单的一字棋（tic-tac-toe）游戏中，这个数量级也相对较大： 存在 $9!=362880$ 个终止节点。

所以我们必须要进行一定的手段来对搜索空间进行限制，来保证搜索的实际可行性。 具体的思路是，我们其实不必要遍历所有的点，因为很多点是必然不会经历/不需要考虑的。 例如下图，虚线框的值不必考虑，因为 C 节点的 minimax 值必然小于 2（Min 只会选取最小节点），所以在 A 节点上选取是必然不会考虑 C 节点。

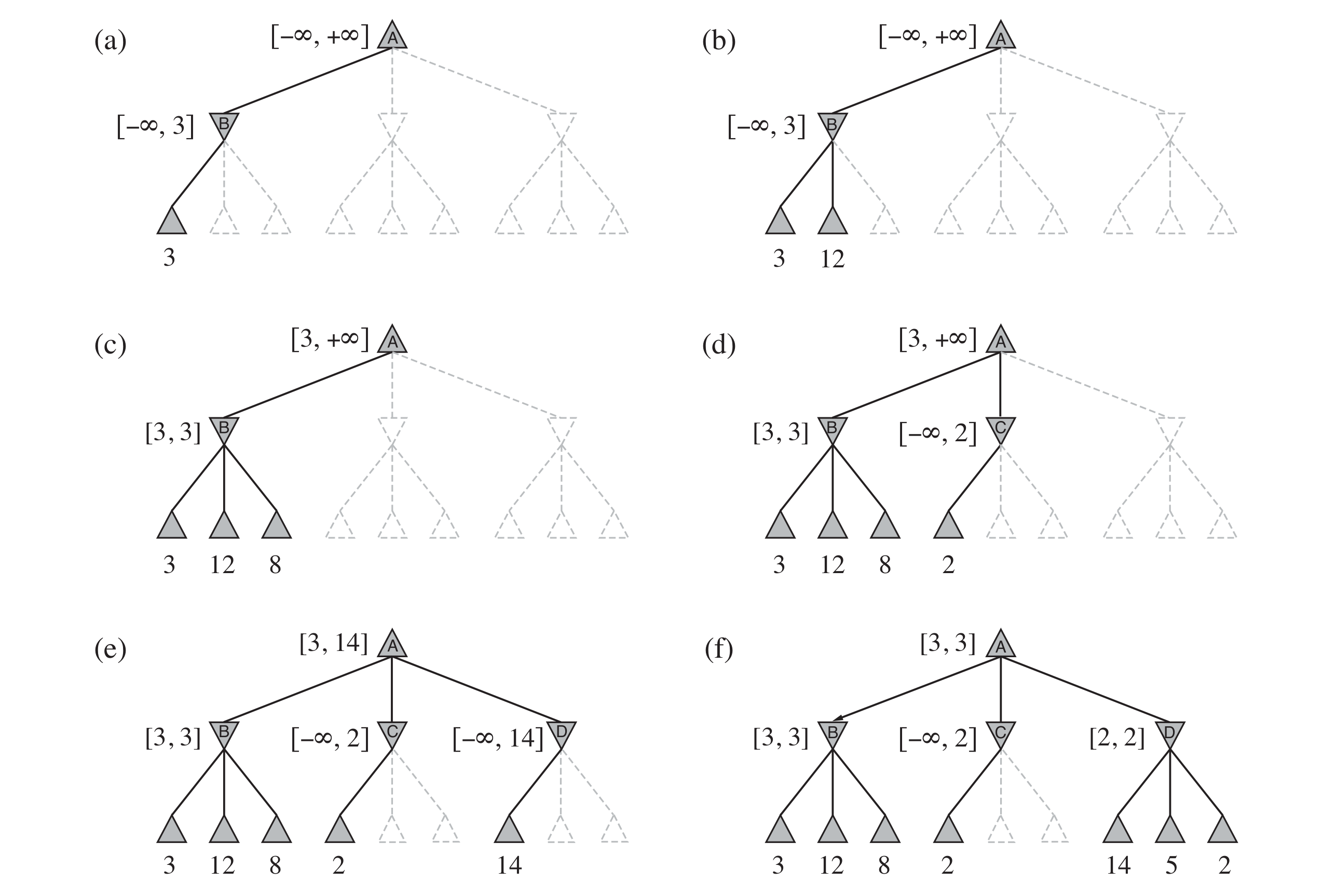
所以，在此算法上：

• 对于每一个节点，我们维护一组上下限 $[\alpha, \beta]$，表示在当前节点 Minimax 值的范围，初始设置为 $[-\infty, \infty]$。[Max 至少能实现的收益, Max 最多能实现的收益]
• 对于一个 Max 节点 $s_{max}$，我们向上更新他的 $\alpha$ 值，将其子节点 $m$ 的 $\beta(m)$ 值与当前的 $\alpha$ 做比较：
  • 如果 $\beta(m) \leq \alpha$，则后续分支可以剪掉（直接 return）。
    • 若 $m$ 的一个子节点 $n$ 上，$\beta(n) \leq \alpha$，则 $\beta(m)$ 必然小于 $\alpha$。
  • 对于 $\beta(m) > \alpha$，则需要更新 $s_{min}$ 上的 $\alpha$ 值。
• 对于一个 Min 节点 $s_{min}$，我们向下更新他的 $\beta$ 值，将其子节点 $m$ 的 $\alpha(m)$ 值与当前的 $\beta$ 做比较
  • 如果 $\alpha(m) \geq \beta$，则后续分支可以剪掉（直接 return）。
    • 若 $m$ 的一个子节点 $n$ 上，$\alpha(n) \geq \beta$，则 $\alpha(m)$ 必然不小于 $\beta$。
  • 对于 $\alpha(m) \lt \beta$，则需要更新 $s_{min}$ 上的 $\beta$ 值。
• 对于叶节点 $k$， $\alpha(k) = \beta(k) = \text{utility}(k, p)$

TIP

即使使用了 alpha-beta 剪枝，在实际中也基本不可能搜索到游戏结束，这就需要使用启发式评估函数 (heuristic evaluation function) 来代替游戏结束时的效用函数，来对一些较深层的状态进行评估，这里不再展开。